wiki - 算法小站

wiki 主题

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

图论

图的连通性

有向图的强连通分量

无向图的割点割边和双连通分量

流和匹配

最大流

最大流的一些应用

最小割

费用流

图论杂项

最大团搜索算法

树上问题

kruskal重构树

kruskal重构树的一些问题

[[ item.c ]]

费用流及应用

## 费用流
**费用流问题**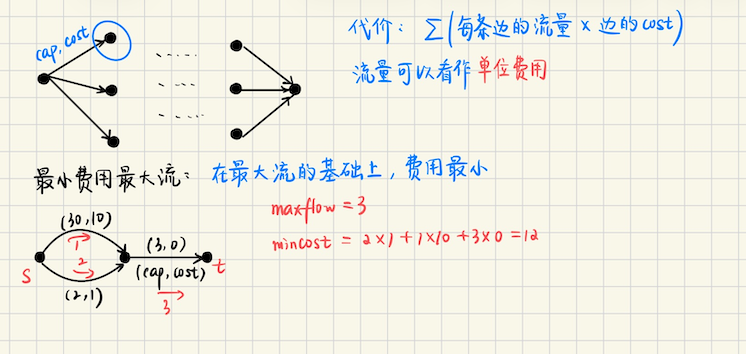
![](/media/content_img/mcmf01.png)
**循环流**
![](/media/content_img/mcmf02.png)

## 最小费用最大流算法
**基于 EK 的 MCMF 算法**
1）构建残量网络，正向边的边权是`cost`，反向边的边权记为`-cost`
反向边相当于**撤销操作**
2）考虑**对流量增广**，沿着最短路（关于费用最小）增广，边权就是**费用**

### 找最短路
找最短路的方法，可以用 SPFA，或者 Johnson 消负权的 dijkstra
#### Johnson 消负权 dijkstra
定义**势函数**$$h(u)$$，保持原图的最短路径相对不变

**添加虚拟原点**
在原图中添加一个虚拟源点$$s$$，并且从$$s$$到**原图的所有节点**添加边权是`0`的边，生成一个新图$$G$$
**新图运行 Bellman-Ford**
从`s`开始跑`SPFA(s)`，计算从`s`到每个节点$$v \in V$$的最短路径距离$$h(v)$$
如果检测到负环，算法终止
**Johnson 消负权**
对于原来的每条边`(u, v)`，定义权重
```math
\displaystyle
w'(u, v) = w(u, v) + h(u) - h(v)
```
**运行 Dijkstra**
在新图上执行`dijkstra(u)`，即可以求出从`u`到所有节点的**调整后的最短路径**
**恢复原路径距离**
```math
\displaystyle
d(u, v) = d'(u, v) - h(u) + h(v)
```

> 证明
新权重，因为我们先执行了一遍`Bellman-Ford`，$$h_v \leqslant h_u + w(u, v)$$
从而$$w'(u, v) = w(u, v) + h(u) - h(v) \geqslant 0$$
这样所有的边都是非负的

> 等价性
新路径的总权重，$$s \to p_1 \to p_2 \cdots \to p_k \to t$$
```math
\displaystyle
(w(s, p_1) + h_s - h_{p_1}) + (w(p_1, p_2) + h_{p_1} - h_{p_2}) + \cdots + (w(p_k, t) + h_{p_k} - h_t) \\
= w(s, p_1) + w(p_1, p_2) + \cdots + w(p_k, t) + h_s - h_t
```
其中$$h_s - h_t$$是定值，所以新路径的总权重等于$$\sum w$$，即原路径的总权重
那么对新图求最短路，自然等于原图

**特别说明**
在最小费用最大流问题中，我们往往是将反向边设置为$$(cap, cost) = (0, -c)$$
在一开始的时候，因为反向边的`cap = 0`，一开始并不会真的跑反向边的负权
那么对应的此时边权都是非负，我们在非负图上确定势能函数`h`
所以在最小费用最大流问题中，一开始可以直接跑 dijkstra，而不必先跑 spfa

**算法实现**
```bash
template <typename T>
class Graph {
public:
    struct _Edge {
        int from;
        int to;
        T cap;
    };
    int _n;
    vector<_Edge> e;
    vector<vector<int> > g;
    vector<T> dis;

// 用于 Johnson 消负权，虚源默认是 0
    int src = 0;
    vector<T> h;
    // Johnson 消负权所需要的 info
	// 其余代码省略
	
    bool JohnsonPre() {
        // 只调用一次，获取势能
        // 实现的时候正常加边，不加虚源，johnson 所需的源节点在 Johnson 方法中考虑
        // src to all nodes, w(src, u) = 0
        for (int u = 1; u <= this->_n; u++) addEdge(src, u, 0);
        if (spfa(src) == false) return false;
        this->h = this->dis;

// 备份边表，调整边表
        for (auto &[from, to, cap] : e) {
            cap += h[from] - h[to];
            // assert(cap >= 0);
        }
        return true;
    }
    void Johnson(int s) {
        dijkstra(s);
        for (int u = 0; u <= this->_n; u++) {
            if (dis[u] < inf<T>) {
                dis[u] = dis[u] + h[u] - h[s];
            }
        }
    }
    void JohnsonDone() {
        // 恢复原来的边权
        for (auto &[from, to, cap] : e) {
            cap -= h[from] - h[to];
        }
    }
};
```
#### MCMF 算法实现
**关于负环**
负环是可能存在的，但是绕负环的时候，必须要有**流**过去，可能一次增广之后
这条边就满流了（相当于从残量网络中删掉），满流之后负环就绕不了了

在负环上，绕行的流量只能是$$\max |f|$$（负环上最大边的流量），绕完之后就不会再进入负环了
（可以看作绕一遍就把负环删掉）

MCMF 默认**初始图**不带负环，有几种情况
1）边权都是正的
2）整个图是一个 DAG

增广之后的残量网络呢？
增广的过程，**最短路是会越来越大**（关于费用的最短路）
> 假设说最短路会变小，那意味着存在撤销操作，既然撤销了，为什么一开始不走那条更短的路？矛盾

**时间复杂度**
时间复杂度是$$O(|f| \cdot \text{spfa})$$，其中$$|f|$$是指增广次数
而`SPFA`的上界是$$O(nm)$$，所以这样做的代价是$$O(|f| \cdot nm)$$

```bash
template<class T>
struct MinCostFlow {
public:
    struct _Edge {
        int to;
        T cap;
        T cost;
        _Edge(int to_, T cap_, T cost_) : to(to_), cap(cap_), cost(cost_) {}
    };
    int n;
    vector<_Edge> e;
    vector<vector<int> > g;
    vector<T> h, dis;
    vector<int> pre;

MinCostFlow() {}
    MinCostFlow(int n_) {
        init(n_);
    }
    void init(int n_) {
        n = n_;
        e.clear();
        g.assign(n+5, {});
    }

void addEdge(int u, int v, T cap, T cost) {
        g[u].push_back(e.size());
        e.emplace_back(v, cap, cost);
        g[v].push_back(e.size());
        e.emplace_back(u, 0, -cost);
    }

bool spfa(int s) {
        dis.assign(n+5, numeric_limits<T>::max());
        pre.assign(n+5, -1);
        vector<bool> inq(n+5, 0);
        vector<int> cnt(n+5, 0);
        queue<int> que;

dis[s] = 0;
        que.push(s), inq[s] = true, cnt[s]++;

while (!que.empty()) {
            int u = que.front(); que.pop();
            inq[u] = 0;

for (int i : g[u]) {
                int v = e[i].to;
                T cap = e[i].cap;
                T cost = e[i].cost;

if (cap > 0 and dis[v] > dis[u] + cost) {
                    dis[v] = dis[u] + cost;
                    pre[v] = i;

if (!inq[v]) {
                        que.push(v), inq[v] = 1, cnt[v] += 1;
                        if (cnt[v] > n) {
                            return true;
                        }
                    }
                }
            }
        }

h.assign(n+5, 0);
        for (int i = 0; i <= n; i++) {
            if (dis[i] != numeric_limits<T>::max()) h[i] = dis[i];
        }
        return false;
    }

bool dijkstra(int s, int t) {
        dis.assign(n+5, numeric_limits<T>::max());
        pre.assign(n+5, -1);

priority_queue<pair<T, int>, vector<pair<T, int> >, greater<pair<T, int> > > que;
        dis[s] = 0;
        que.emplace(0, s);

while (!que.empty()) {
            T d = que.top().first;
            int u = que.top().second;
            que.pop();

if (dis[u] != d) continue;

for (int i : g[u]) {
                int v = e[i].to;
                T cap = e[i].cap;
                T cost = e[i].cost;

if (cap > 0 and dis[v] > d + h[u] - h[v] + cost) {
                    dis[v] = d + h[u] - h[v] + cost;
                    pre[v] = i;
                    que.emplace(dis[v], v);
                }
            }
        }

return dis[t] != numeric_limits<T>::max();
    }

pair<T, T> flow(int s, int t, bool use_spfa = false) {
        T flow = 0;
        T cost = 0;

if (use_spfa) {
            bool neg = spfa(s);
            if (neg) {
                return make_pair(-1, -1);
            }
        }
        else {
            h.assign(n+5, 0);
        }

while (dijkstra(s, t)) {
            for (int i = 0; i <= n; i++) {
                if (dis[i] != numeric_limits<T>::max())
                    h[i] += dis[i];
            }

T aug = numeric_limits<T>::max();
            for (int i = t; i != s; i = e[pre[i] ^ 1].to) {
                aug = min(aug, e[pre[i]].cap);
            }

for (int i = t; i != s; i = e[pre[i] ^ 1].to) {
                e[pre[i]].cap -= aug;
                e[pre[i] ^ 1].cap += aug;
            }

flow += aug;
            cost += aug * h[t];
        }

return make_pair(flow, cost);
    }

struct Edge {
        int from;
        int to;
        T cap;
        T cost;
        T flow;
    };

vector<Edge> edges() {
        vector<Edge> a;

for (int i = 0; i < e.size(); i += 2) {
            Edge x;
            x.from = e[i+1].to;
            x.to = e[i].to;
            x.cap = e[i].cap + e[i+1].cap;
            x.cost = e[i].cost;
            x.flow = e[i+1].cap;
            a.push_back(x);
        }
        
        return a;
    }
};
```

#### Label-Correcting

> 特别说明

其实`SPFA`方法**可以不要**，默认`flow(s, t, use_spfa = false)`也可以正确运行，因为在`dijkstra`中
```bash
if (cap > 0 and dis[v] > d + h[u] - h[v] + cost) {
    dis[v] = d + h[u] - h[v] + cost;
    pre[v] = i;
    que.emplace(dis[v], v); // 再次入队
}
```
用了 **Label-Correcting 算法**
```bash
if (dis[u] != d) continue;
```
也就是说，如果一个节点$$u$$**之前被处理过**，后来发现可以经过一条负权边再次到达它
那么`u`的`dis`会被再次更新，并且进入队列

只要没有**负环**，那么这种**允许反悔**的`dijkstra`实际上执行的是类似`SPFA`，最终会收敛
**SPFA**方法许多时候是用来判负环的，但是费用流问题中，增广会流干环中的流量
而这相当于删除环中的边，所以一般是没有什么问题的

由于`dijkstra`允许节点被反复更新，它在第一次迭代中实际上扮演了 SPFA 的角色，硬扛着负权边算出了正确的最短路`dis`
随后用`dis`来算出势能函数`h`，就是`Johnson`消负权的过程

## 运输问题
**[运输问题](https://www.luogu.com.cn/problem/P4015)**
给定$$m$$个仓库和$$n$$个零售店，其中第$$i$$个仓库有$$a_i$$的货物
第$$j$$个商店需要$$b_j$$个单位的货物

货物供需平衡，$$\sum a_i = \sum b_j$$
从第$$i$$个仓库运送每单位货物到$$j$$个零售商店，需要$$c(i, j)$$的费用
设计一个运输方案，使得总的运输费用最少

**算法分析**
很裸的费用流，左右两排点
左边一排点$$i$$，与$$s$$连边$$(s, i, a_i)$$，`cost = 0`的边，流量上限$$a_i$$表示能**提供**这么多货物
右边一排点$$i$$，与$$t$$连边$$(i, t, b_i)$$，`cost = 0`，流量上限表示**需要**$$b_i$$这么多货物
中间每一对$$(i, j)$$，连边$$(+\infty, c(i, j))$$，流量上限是$$+\infty$$，费用是$$c(i, j)$$

对这个图跑一遍最小费用最大流即可
最大费用呢？`cost = -cost`，跑一遍最小费用最大流

## 数字梯形问题
**[数字梯形问题](https://www.luogu.com.cn/problem/P4013)**
```bash
				2		3
			3		4		5
		9		10		9		1
	1		1		10		1		1
1		1		10		12		1		1
```
第一行有`m`个数字，从顶部开始，每个数字处可以左下或者右下移动
形成一条从顶部到底部的路径

但是有要求
1）顶到底的`m`条路径不相交
2）顶到底的`m`条路径仅仅在数字节点处相交
3）顶到底的`m`条路径可以在数字节点处，或者边相交

输出这三种情况下，最大的数字总和

**算法分析**
可以考虑**用流来表示路径**，第一排的点，每个点都要往下走
对于第一排的每个点$$i$$，从$$s \to i$$分发`1`的流量

接下来考虑限制，**卡点的流量**和边的流量
一个点能被经过多少次，流量就设为多少，卡点的流量和费用，**拆点**即可
边也是类似的，一条边可以被经过多少次，流量就设为多少

1）考虑拆点，对$$(u, u')$$，在情况1中，一个点只能被经过一次，`cap = 1, cost = c[u]`
（流量上限设为`1`，费用就是这个数的值）
对于情况`2, 3`，一个点可以**被经过多次**，流量上限设为$$+\infty$$，费用同样是这个点的数值

2）考虑行与行之间，（即题目中所谓的边），情况`1, 2`，边只能经过一次
所以$$(u', v)$$连流量上限是`1`的边，费用为`0`（只有经过拆点才会产生费用）
对于情况`3`，边的流量上限设为$$+\infty$$，费用是`0`

3）终点处，即最后一行，可能会有多条路径汇聚在一个点结束，最后一行的点向汇点$$t$$连边
流量可以是$$+\infty$$

## K 取方格数
**[K 取方格数](https://www.luogu.com.cn/problem/P2045)**
给定一个$$n \times n$$的矩阵，每一格有一个非负整数$$A\_{i, j}$$
现在从$$(1, 1)$$出发，往右边或者往下走，最后到达$$(n, n)$$，每到达一个方格
就把格子中的数取出来，这样格子中的数就变成`0`，一共走`K`次
要求`K`次所到达的方格的数的和最大

**算法分析**
> 问题一，第一次经过`+x`，后面可以多次经过`+0`，这怎么建模

之前的问题，一个点能允许经过几次，`cap`就等于几，如果只能经过一次的话，`cap = 1`
花费的代价是`x = a(i, j)`
如果一个点能被多次经过，$$cap = +\infty$$，在这个问题中，多次经过费用设为`0`

对`u`**拆点**，$$(u, u')$$连两条边，一条是流量`1`费用`a(i, j)`，另一条是流量$$+\infty$$费用`0`

这样增广$$|f|$$次，最大费用流会优先考虑费用最小的边，也就是沿着$$a\_{i, j}$$先走
流量耗尽之后，才考虑走$$(flow, cost) = (+\infty, 0)$$的边

其实这个问题还可以扩展，比如第一次经过**费用**是$$x_1$$，第二次经过**费用**是$$x_2$$
以此类推，第$$n$$次经过费用是$$0$$，要求$$x_1 \geqslant x_2 \cdots \geqslant 0$$
这也是可以做的，根据贪心性质，如果有流的话，一定是先考虑**费用最大**的边去流
考虑建边`(flow, cost)`，依次是$$(1, x_1), (1, x_2), \cdots, (+\infty, 0)$$

> 问题二，怎么对$$1\sim n$$输出答案

费用流，增广`1`的流量就代表一条路径，`2`的流量就代表有`2`条路径
对每次增广都输出答案即可

在`flow`的`augment`中，每次只增广`1`的流量
```bash
vector<T> totcost;

while (dijkstra(s, t)) {
	for (int i = 0; i <= n; i++) {
		if (dis[i] != numeric_limits<T>::max())
			h[i] += dis[i];
	}

T aug = 1
	// 增广代码省略

flow += aug;
	cost += aug * h[t];

totcost.emplace_back(cost);
}

return make_pair(flow, totcost);
```

## 餐巾计划问题
**[餐巾计划问题](https://www.luogu.com.cn/problem/P1251)**
一个餐厅，第`i`天需要$$r_i$$块餐巾，有如下选择
1）购买新餐巾，费用是$$c_0$$
2）旧的餐巾送到快洗部，洗一块餐巾要$$d_1$$天，费用是$$c_1$$
3）旧的餐巾送到慢洗部，洗一块餐巾要$$d_2, (d_2 > d_1)$$天，费用是$$c_2 (c_2 < c_1)$$

每天结束，餐厅决策需要多少块餐巾送到快洗部，多少块餐巾送到慢洗部
还需要决策保存多少餐巾延期送洗
限制是，每天洗好的餐巾和购买的餐巾之和，$$\geqslant r_i$$至少要满足当天需求

设计算法，安排`n`天餐巾使用计划，使得总花费最小

**算法分析**
考虑建图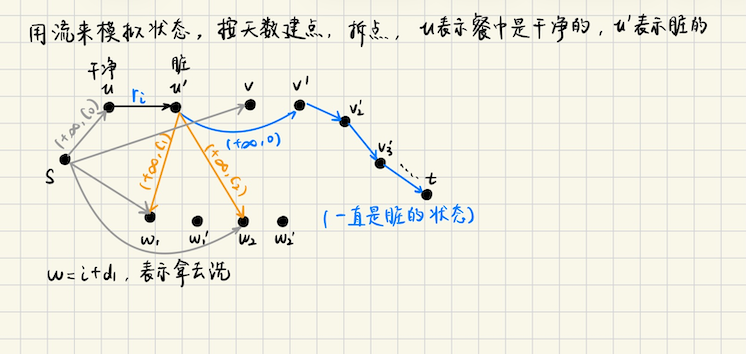
![](/media/content_img/mcmf03.png)

但很可惜，这个问题不能等同于**最大流**
之前的流网络问题中，都是**每天最多能用**$$r_i$$张餐巾，现在呢？是**至少**需要$$r_i$$
每条边有一个**流量下界**$$\geqslant r_i$$

那么这个问题对应**最小费用可行流**

### 最小费用可行流

注意，可行流并不要求流要最大

如果我们要求$$(u, v)$$**至少要流满**$$r_i$$怎么办？
对于$$(u, v)$$，可以考虑`(flow, cost)`连边$$(r_i, -\infty)$$，连一条费用是$$-\infty$$的边
那么对流网络求最小费用即可

如果$$(u, v)$$不满流，答案一定不是最优的
因为走$$(u, v)$$这条边的代价是$$-\infty$$非常小，直接流满$$(u, v)$$是划算的

所以对于有下界的情况，$$\geqslant d_u$$，加入边$$(d_u, -\infty)$$跑最小费用
让这条边满流，就满足了下界的情况
（如果不要求流最大，那么$$-\infty$$费用的边流量拉满之后就可以了）

**特别说明**，对于有下界的流，比如说$$\geqslant r_i$$
1）有的题目，比如本题，一天恰好用了$$r_i$$的餐巾就是最优的，所以让$$r_i$$满流即可
连边$$(flow, cost) = (r_i, -\infty)$$

2）而有的题目，达到了下界$$r_i$$之后，还需要继续流
那么可以再添加一条$$(flow, cost) = (+\infty, 0)$$，表示满流后可以随便流，不需要额外费用

> 具体怎么求最小费用可行流呢？

之前求最小费用最大流的时候，是在最大流的基础上求的，也就是说，没有增广路的时候停止`SPFA`
那么**最小费用可行流**，增广路长度$$dis(t) \geqslant 0$$**直接停掉**，不再增广

> 因为**可行流**，在任何时刻流量$$f \geqslant 0$$，而最短路是**关于费用的**最短路
如果$$dis(t) \geqslant 0$$，说明**费用大于 0**，再继续增广的话，费用会越来越大

**最后怎么计算答案？**
计算答案的时候，注意我们添加了$$(r_i, -\infty)$$的边，来辅助这条边满流
实际上这部分流量是没有的，$$ans += (\sum r_i) \cdot |\infty|$$才是实际的答案

```bash
pair<T, T> flow(int s, int t, bool use_spfa = false) {
	// 前面代码省略
    while (dijkstra(s, t)) {
        for (int i = 0; i <= n; i++) {
            if (dis[i] != numeric_limits<T>::max())
                h[i] += dis[i];
        }

// 如果是最小费用可行流，加下面一句话，在 h[t] >= 0 的时候直接停止增广
        if (h[t] >= 0) break;

T aug = numeric_limits<T>::max();
		// 增广过程省略
    }

return make_pair(flow, cost);
}

void solve() {
	auto [flow, cost] = g.flow(s, t);
	cost += sumr * INF;
}
```
## 一般可行流问题
**供应-需求模型**
![](/media/content_img/mcmf04.png)
**回到餐巾计划问题**
![](/media/content_img/mcmf05.png)

## The Most Reckless Defense
**[H. The Most Reckless Defense](https://codeforces.com/problemset/problem/1955/H)**
给定$$n \times m$$个网格，有$$K$$个塔防，并且给定一条敌人会经过的路径
如果敌人在$$(x, y)$$，并且塔防在$$(x_i, y_i)$$，攻击范围是$$r$$，满足$$(x - x_i)^2 + (y - y_i)^2 \leqslant r^2$$
此时敌人会受到$$p_i$$点伤害，塔防$$(x_i, y_i, p_i)$$是给定的，攻击范围$$r$$你可以自己选

但是有限制，一开始所有塔防的攻击范围$$r = 0$$，假设敌人基础生命值是$$h$$
那么你设置塔防的攻击范围$$r > 0$$，敌人的生命值会$$+3^r$$
攻击范围的选择，在敌人出现前一次性确定，比如选`3`个塔防，$$r = 2, 4, 5$$
敌人的生命值$$h + 3^2 + 3^4 + 3^5$$，塔防攻击范围在游戏开始前选定，中途不能更改
另外，**每一个`r`最多只能被一个塔防使用**

如果敌人到达$$(n, m)$$还没有被消灭，玩家失败，否则玩家成功
现在求玩家不会失败的最大的$$h$$

**算法分析**
1）注意到塔防能够产生最大的生命伤害量是$$p_i \cdot \pi r^2 = O(500\pi r^2)$$
那么敌人最多能够获得的额外生命是$$3^r$$，$$500 \pi r^2 \geqslant 3^r, r \leqslant 12$$
可以发现`r`的值不会很大，最多就是`12`

2）另外，根据提示，每个`r`最多只能被一个塔防使用，不难发现很**类似网络流的匹配**

3）根据题目中样例`3`的解释，塔防$$i$$在`(1, 2)`处，如果设定半径是`r = 2`
能够覆盖“敌人经过路径”的长度是$$d_i = 3$$，所以可以造成的伤害是$$p_i d_i = 1500$$
而敌人额外生命是$$3^2 = 9$$，那么这一组$$(i, r)$$对答案的贡献就是$$p_i d_i - 3^r$$

4）那么可以考虑$$(i, r)$$连一条流量为`1`，费用是$$p_id_i - 3^r$$的边
从`(s, i)`连一条流量是`1`，费用为`0`的边
从`(K+r, t)`连一条流量是`1`，费用为`0`的边
对这个图跑**最大费用流**即可（为了达成这个目的，费用设成$$-(p_id_i - 3^r), d_i$$可预处理）

至于什么时候答案是`0`呢？实际上，费用$$cost = p_id_i - 3^r$$
因为我们添加的是**费用的相反数**来求最大费用流，如果$$cost \leqslant 0$$就不添加这条边了

**还有一个坑点**
这个题目不要求最大流，也就是说，可以允许一部分的`r, i`没有匹配上
是一个**最大费用可行流**问题，因为我们有$$< 0$$的费用的边
在增广的时候，遇到$$h(t) \geqslant 0$$就停止增广即可

看完文章有啥想法

算法小站

wiki 主题

图论

费用流及应用

目录