算法小站

首页wiki新鲜事文章搜索网站导航回忆录
算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

wiki 主题

二维偏序高维前缀和树上差分中位数定理搜索线段树单点修改线段树区间修改动态开点线段树线段树的合并（一）可持久化线段树树链剖分FHQ-Treap珂朵莉树位分块根号分治虚树回文串回文树二项式定理生成函数（一）FFT多项式与形式幂级数同余与模的应用同余与模的概念斯特林数斯特林数相关的恒等式斯特林数的综合应用FFT的应用整除分块有向图的强连通分量无向图的割点割边和双连通分量最大流最大流的一些应用最大团搜索算法kruskal重构树kruskal重构树的一些问题背包模型凸壳优化单调队列优化计算几何启发式合并高精度约瑟夫环曼哈顿距离多重集合的排列组合蔡勒公式排列与置换Catalan数与格路径
是否为父主题
是否为其添加wiki文章
取 消 确 定
修改主题名称
修改父主题
修改wiki文章
取 消 删 除 修 改
算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

动态规划

  • 背包模型
  • dp优化
  • 凸壳优化
  • 单调队列优化

    • [[ item.c ]]

    0
    0

    凸壳优化

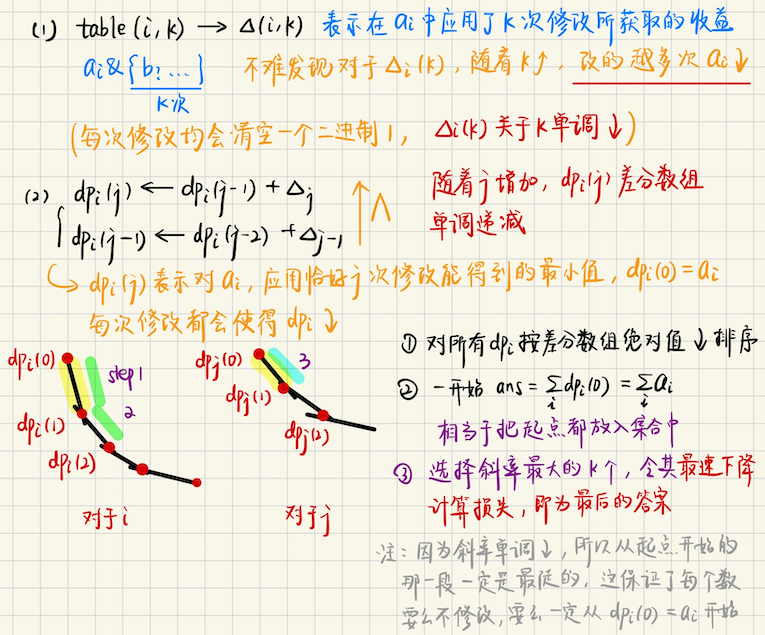
    看完文章有啥想法

    43 人参与，0 条评论

    目录

    [[ item.c ]]