wiki - 算法小站

wiki 主题

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

数据结构

线段树

线段树单点修改

线段树区间修改

动态开点线段树

线段树的合并（一）

可持久化线段树

树链剖分

平衡树

FHQ-Treap

珂朵莉树

分块

位分块

根号分治

虚树

[[ item.c ]]

虚树

## 虚树的引入
**[leetcode 3786. 树组的交互代价总和](https://leetcode.cn/problems/total-sum-of-interaction-cost-in-tree-groups/description/)**
给定一个`n`个节点的树，同时给定一个长度是`n`的数组`col`，`col[i]`表示节点`i`的颜色
现在问，所有同色节点`(u, v)`之间，它的简单路径经过的边数是多少？假设是`cnt`，把`cnt`加到答案里

**算法分析**
> 假设所有点的点权都相同，怎么做？

从边考虑，对每一条边，考虑**它被经过了多少次**，假设是`cnt`，那么这条边对答案的贡献就是`cnt`
（实际上，就是统计经过边$$(u, v)$$的**方案数**）

`cnt`的计算并不困难，$$(u, v)$$，那么只需要在`v`这棵子树中选一个点，方案数是$$|sz(v)|$$
之后，考虑`v`的补集，那么就是$$n - |sz(v)|$$，答案就是$$v \cdot (n - |sz_v|)$$

> 现在多种颜色，怎么办？

注意到颜色的数量不是很多，那么可以**每个颜色开一个桶**，假设当前考虑`col`
我们可以很方便的统计`col`的节点一共有多少个`tot[col]`
那么贡献就是`cnt[v, col] * ( tot[col] - cnt[v, col] )`

### 树的压缩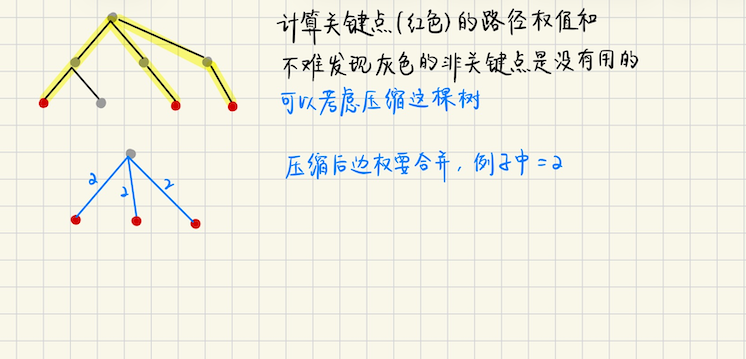
![](/media/content_img/virtualTree01.png)

## 虚树的构建，二次排序

> 算法流程

1）对所有的关键点依据`dfs 序`排序
2）相邻的关键点之间的`LCA`加入序列，再一次按照`dfs 序`排序
3）每一组相邻点`LCA = (last, now)`，对于当前考虑的`now`，连边`(LCA, now)`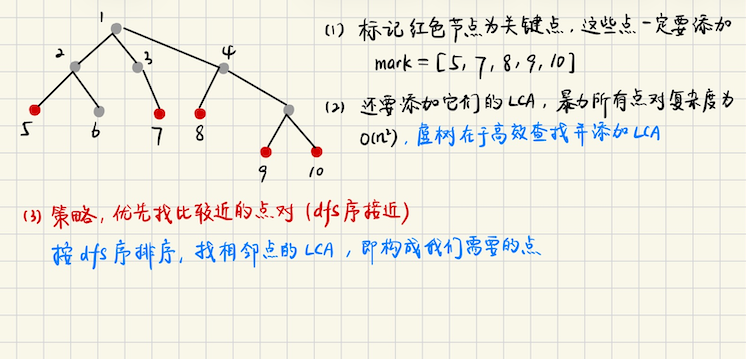

![](/media/content_img/virtualTree02.png)
![](/media/content_img/virtualTree03.png)

**连边之后注意点**
1）权值要改，边权可能不再是`1`了，而是**深度差**，$$|dep_u - dep_v|$$
2）统计答案贡献的时候，注意只能统计**有标记的关键点**，而我们另外添加的**LCA 可能无贡献**

### Educational Codeforces Round 162
#### E
**[E. Count Paths](https://codeforces.com/contest/1923/problem/E)**
给定一个`n`个节点的树，每个点都被染色，颜色用$$1 \sim n$$表示
一条树上的简单路径，被称为美丽路径，当且仅当
1）路径上至少有`2`个点，起点和终点的颜色相同
2）路径上的其他点，都不和起点的颜色相同

计算美丽路径的数量，$$n \leqslant 2\cdot 10^5$$，路径无向的，`x->y, y->x`被视为同一条路径

**算法分析**
假设当前考虑颜色$$c$$，将`color = c`的节点视为关键点构建出虚树，不难发现
**限制一**
路径的起点和终点，一定要在虚树上，并且是**关键点**
考虑在虚树上跑**树形 dp**

记$$dp_u$$表示`u 及其子树`**合法路径**的方案数，那么`dfs(u)`时
1）如果`u`不是关键点，那么就一定是`LCA`，合法路径一定分别位于`u`的两棵子树中，`u`的贡献
（指经过`u`的合法路径）
```math
\displaystyle
\sum_{i \neq j} dp(v_i) dp(v_j)
```
**这样的式子怎么计算呢？任意两个数的乘积，求他们的和**

有一个很快的算法，$$\sum\_{i \neq j}x\_i x\_j = \dfrac{(x\_1 + x\_2 + \cdots x\_m)^2 - (x\_1^2 + x\_2^2 + \cdots + x\_m^2)}{2}$$

```math
\displaystyle
\sum_{i \neq j} dp(v_i)dp(v_j) = \left(\sum_{i} dp(v_i) \right)^2 - \sum_i\left( dp(v_i)^2 \right)
```

把上述贡献加到答案中即可
转移呢？此时`子树 v 原来的合法路径`，都还能称为合法路径，$$dp(u) = \sum dp(v)$$

2）如果`u`是关键点，首先，虚树中的叶子结点一定是关键点，如果`u 不是叶子结点`，对于分支$$v$$
那么合法路径只能在`v`的子树中，不能跨过`v->u`到其他分支中

此时`u`的贡献是多少呢？要经过`u`，**就只能以`u`作为路径端点**

**观察一**
注意到`dp(u)`等价于，路径经过`u`，并且**端点只能在`u`的子树中选，**此时端点选择的方案数
问题要求端点必须是关键点，所以`dp(u)`实际上就是`u 及其子树中`**合法的关键点**

**观察二**
因为要求路径中没有其他关键点，所以`dp(u)`只能统计，在每个分支$$v$$中，**离`u`最近**的那个关键点
这个怎么做呢？
其实不难，**在回溯的时候**，如果`u`是关键点，统计完答案之后，**把`u 的子树删掉，只放入 u 这一个点`**即可
对应的操作就是统计完答案， 回溯时$$dp(u) = 1$$，这就是**状态转移**

最后，怎么统计答案呢？`dfs( u 是关键点 )`的时候，此时`u`要想贡献答案，`u`就必须是路径的端点

那么路径的另一端有几种选法呢？恰好是$$\sum dp(v)$$，所以答案就是$$ans += \sum dp(v)$$
然后我们令$$dp(u) = 1$$，继续回溯

> **注意！！！**

1）在虚树的构建中，必须声明成为`static Virtree vt`，要不然每一次`adj, mark`都会被初始化为$$O(n)$$
2）在`build`之前，需要清空`clear()`树中的节点，这最好放在`build`成员函数里执行
否则不合法的情况，可能还会往`nodes`里堆数据
3）如果虚树建出来之后需要`dp`，切记！`adj, mark`按引用传递，而不是拷贝整棵树
另外，`dp`数组**必须`static dp`**，只初始化**用到的节点**$$x, dp_x = 0$$

#### 算法实现
```bash
void solve(int cas) {
    int n;
    cin >> n;

vector<int> c(n+1, 0);
    for (int i = 1; i <= n; i++) cin >> c[i];

vector<vector<int> > g(n+1);
    for (int i = 0; i < n-1; i++) {
        int x, y;
        cin >> x >> y;
        g[x].emplace_back(y), g[y].emplace_back(x);
    }

HLD hld(1, g);

vector<vector<int> > ver(n+1);
    for (int u = 1; u <= n; u++) ver[c[u]].emplace_back(u);

// static 很重要
    static Virtree vt;
    vt.init(n);

i64 ans = 0;
    for (int col = 1; col <= n; col++) {
        if (ver[col].size() < 2) continue;
        vt.build(hld, ver, col);

const auto &mark = vt.mark;
        const auto &adj = vt.adj;

// dp 不能 O(n) 初始化, static 的，只标记用到的节点
        static vector<i64> dp;
        dp.resize(n+1);

for (int x : ver[col]) dp[x] = 0;

auto dfs = [&](auto &dfs, int u, int fa) -> void {
            i64 sdp = 0, sdp2 = 0;

for (auto v : adj[u]) {
                if (v == fa) continue;
                dfs(dfs, v, u);
                sdp += dp[v], sdp2 += dp[v] * dp[v];
            }

if (!mark[u]) {
                i64 dpv = (sdp * sdp - sdp2) / 2;
                ans += dpv;
                dp[u] = sdp;
            }
            else {
                ans += sdp;
                dp[u] = 1;
            }
        };

dfs(dfs, 1, 0);
    }

cout << ans << "\n";
}
```
## 虚树的构建：单调栈
![](/media/content_img/virtualTree04.png)
### 算法实现
```bash
struct Virtree {
    int n = 0;
    vector<vector<int> > adj;
    vector<int> mark;
    vector<int> nodes;
    // ins 是辅助数组，判断哪些点已经被加入虚树
    vector<int> ins;
    int root = 1;

Virtree() = default;
    Virtree(int n) {
        init(n);
    }

void init(int _n) {
        if (_n <= n) return;
        n = _n;
        adj.assign(n+1, {});
        mark.assign(n+1, 0);
        ins.assign(n+1, 0);
    }

void build(const VirtreeBase &tree, const vector<vector<int> > &ver, int color) {
        this->clear();

vector<int> key = ver[color];
        if (key.empty()) return;

// sort, according to dfn
        sort(key.begin(), key.end(), [&](int a, int b) {
            return tree.l[a] < tree.l[b];
        });

// mark
        for (auto x : key) mark[x] = 1;

vector<int> st;
        st.reserve(key.size());

vector<int> all;
        all.reserve(key.size() * 2);

auto addEdge = [&](int x, int y) {
            adj[x].emplace_back(y);
            adj[y].emplace_back(x);
        };

st.emplace_back(key[0]), all.emplace_back(key[0]);
        ins[key[0]] = 1;

for (int i = 1; i < (int)key.size(); i++) {
            int u = key[i];
            int lca = tree.LCA(u, st.back());

while (st.size() >= 2 and tree.dep[st[st.size()-2]] >= tree.dep[lca]) {
                addEdge(st[st.size()-2], st.back());
                st.pop_back();
            }

if (st.back() != lca) {
                if (!ins[lca]) {
                    ins[lca] = 1, all.emplace_back(lca);
                }
                addEdge(lca, st.back());
                st.back() = lca;
            }

st.push_back(u);
            if (!ins[u]) {
                ins[u] = 1, all.emplace_back(u);
            }
        }

while (st.size() > 1) {
            addEdge(st[st.size()-2], st.back());
            st.pop_back();
        }

root = st[0];

this->nodes = all;
    }

void clear() {
        for (auto x : nodes) {
            ins[x] = 0;
            mark[x] = 0, adj[x].clear();
        }
        nodes.clear();
    }
};
```
## 王国和城市
**[D. Kingdom and its Cities](https://codeforces.com/problemset/problem/613/D)**
给定`n`个点的树，`q`个询问，每个询问如下
```bash
k a1 a2 ..... ak
给出 k 个不同的重要点，其他点是非重要点
```
你可以攻占非重要点，被攻占的点无法通行，要让重要点之间两两不连通
打印至少要攻占几个非重要点
如果攻占非重要点不能达成目标，输出`-1`

**算法分析**
首先如果有两个点都是重要点，且相邻，不论如何都不可能，输出`-1`

接着虚树上跑树形`dp`，其中$$dp(u)$$表示使得`u`及其子树合法需要花费的最小代价
（这里的代价指需要攻占几个非重要点）

**情形一**
如果`u`是非重要点，什么时候`u`会被攻占呢？那一定是`u`连着$$\geqslant 2$$的**分支**
并且这些分支都有**未被断开的重要点**
所以我们需要用`has[u]`来维护$$u$$及其子树中，**是否存在**没有断开的重要点（指没有和父亲断开）
`has[u] = {0, 1}`，值只会是`0 or 1`

对于$$u$$，首先必须的代价就是$$base = \sum dp(v)$$
1）此时看一下$$cnt = \sum has(v)$$，如果$$cnt \geqslant 2$$，那么直接贪心地攻占`u`这个点就可以了
代价是$$dp(u) = \sum dp(v) + 1$$，然后`has[u] = 0`

2）如果$$cnt \leqslant 1$$，那么只有一个分支有重要点，此时$$dp(u) = base$$，**不需要额外代价**
至于未断开的那个点，直接往上回溯，**在祖先的重要节点处结算**（如果有）

**情形二**
如果`u`是重要点，那么`u`自己是不能被攻占的，$$base = \sum dp(v)$$仍然是必须的
只需要考虑`has(v) = 1`的那些分支，那些分支是一定要断开的
所以代价就是$$\sum dp(v) + \sum has(v)$$，然后令`has[u] = 1`

这里一定可以断开，因为一开始我们保证了没有两个相邻的重要点，所以在祖先重要点处
一定可以断开，然后结算代价

## 大工程
**[P4103 [HEOI2014] 大工程](https://www.luogu.com.cn/problem/P4103)**
一共有`n`个节点的树，如果在`a, b`之间建立新通道，代价是这两个节点在树上的距离
一共有`q`个查询，每条查询如下
```bash
k a1 a2 ... ak
```
给定`k`个不同的节点，任意两个节点之间都会建立新通道，求新通道的代价和
新通道的代价最小值，新通道中代价最大值

**算法分析**
只需要关心有关键点的那些子树，先考虑怎么计算所有新通道的代价和
> 代价和计算，$$dp(u)$$表示`u`的子树**已经遍历过的分支**到$$u$$的距离之和

先考虑$$v \to u$$，$$dp_v$$和$$dp_u$$是怎么**合并**的
不难发现`u, v 的距离`$$D = |dep(u) - dep(v)|$$
原来所有合法点对到`v`的距离只和是$$dp(v)$$，随着`v 合并到 u`，原来每一个合法的距离
都会`+ D`，一共的增量是$$D \cdot |sz_v|$$，其中$$sz_v$$表示`v 及其子树`有几个关键点

转移如下，$$dp(u) += dp(v) + D \cdot |sz_v|$$

接下来考虑$$u$$**是否结算**，以及结算的代价，一般来说，我们都是在`LCA`处结算
现在假设`u`作为路径的`LCA`是否结算呢？

1）`u`作为非关键点
1.1）若`u`只有一个分支，不需要结算
1.2）若`u`有$$\geqslant 2$$个分支，结算的代价呢？假设现在正在考虑$$v$$这个**子树分支**
并且`v`**还没有并入**`u`中，已经考虑过的分支的距离之和，用`dp(u)`维护起来了

那么分别考虑贡献，首先`dp(u)`的贡献会变成多少呢？不难发现，每一个`dp(u) 维护的关键节点`
**都要去往`v`中**，所以$$+= dp_u \cdot sz_v$$
同理，$$+= dp_v \cdot sz_u$$

另外，$$D = (u, v)$$是新加进来的，它的贡献是多少呢？那恰好等于`端点可以选择的方案数`
端点一边在$$u$$中选，一边在$$v$$中选，$$+= \binom{sz_u}{1} \binom{sz_v}{1} \cdot D$$

所以有$$\Delta = dp_u \cdot |sz_v| + dp_v \cdot |sz_u| + |sz_u| |sz_v| \cdot D$$
结算时候，$$ans += \Delta$$

只有一个分支的情况，那么`sz[u] = 0, dp[u] 在初次遍历的时候也是 0`，所以上面公式恰好可以包含两种情况

2）`u`作为关键点，和前面的情况大差不差，为什么呢？
首先，`u`作为关键点，同时又是`LCA`，跨分支的路径按上面讨论即可正确计算
现在问题是，能否正确计算出单分支的路径呢？

注意到，当还没有合并任何一个分支`v`的时候，贡献是$$dp_v + D \cdot sz_v$$
这能不能正确加入到答案中呢？答案是可以的
**因为这相当于初始时候，有个虚拟分支只有`u`这一个点**，对应前面$$\Delta$$中$$sz_u = 1$$的情况

所以两种情况可以用$$ans += dp_u \cdot |sz_v| + dp_v \cdot |sz_u| + |sz_u| |sz_v| \cdot D$$统一起来

> 怎么维护`mx(u), mn(u)`，实际上就是求经过`u`的树的直径，限制就是**端点必须是关键点**

类似树的直径，定义$$mx(u)$$表示已考虑（合并）的分支中，`u`到子树中的**关键点的最远距离**
```bash
// 维护答案
chmax(ansmx,  mx[u] + mx[v] + D )
// 合并分支
chmax(mx[u], mx[v] + D)
```
对应的`mn[u]`也是类似

## 消耗战
**[SDOI2011 消耗战](https://www.luogu.com.cn/problem/P2495)**
给定`n`个节点的树，每条边有边权，`q`个询问
```bash
k a1 a2 ..... ak
```
给出`k`个关键点，并且一定不包含`1`号节点，可以随意选择边进行切断
切断的代价就是边权，目标是让所有关键点都无法到达`1`号点，求最小代价

**算法分析**
考虑虚树，首先，虚树的边权怎么建？两个关键点$$(u, v)$$，如果`addEdge`的话
边权一定是$$\min(u \to v)$$，取`u, v`路径上**最短的一条边**作为边权
这可以用**树上倍增**来实现

接着考虑`虚树 dp`，考虑`dfs(u)`，定义$$dp(u)$$表示`u 的子树中（不包括 u）`
**所有的关键点**都连不到`u`，此时所需要的最小代价，转移如下

1）如果`v`**是关键点**，那么$$(u, v)$$一定要断开，$$dp(u) += w(u, v)$$
2）否则呢，有两种决策，第一种是$$(u, v)$$不动，我让所有`子树的关键点`都连不到`v`，即`dp(v)`
或者呢，你连不连到$$v$$无所谓，我只需要断开$$(u, v)$$这一条边就可以了
那么转移是$$dp(u) += \min (w(u, v), dp(v))$$

## 世界树
**[HNOI2014 世界树](https://www.luogu.com.cn/problem/P3233)**
给定`n`个节点的树，`q`个询问，每条询问给出
```bash
k a1 a2 ... ak
```
给定`k`个不同的管理点，树上的每个点，都找离自己最近的管理点来管理自己
如果某个节点的最近管理点有多个，选择编号最小的管理点
对每个管理点，输出需要管理的节点的数量

**算法分析**
> 怎么计算一个节点最近的管理点？好像可以在原树上暴力

对于一个点来说，距离最近的管理点，要么在子树中，$$dp(u) = \min (dp(v)) + 1$$
（dp 维护距离）
要么呢？在这个点**往上到父亲中去找**，换句话说，是**子树的补集**
这个用换根 dp，很容易求出来，两次 dfs 即可，第二次用父亲的`dp(fa)`来更新`dp(u)`

这样就可以维护出`to[u]`表示离`u`最近的管理点了

> 因为`q`次询问，每次的关键点会变，需要考虑建出虚树后再`dfs`
那么虚树上怎么统计答案呢？

**虚树上的点**
首先，在虚树上跑 dp，可以算出虚树上每个点对应的管理点
接着考虑怎么对应回原树，难点是，假设说虚树的边$$(u, v)$$，`u <---> v`中间**在原树中**可能隔着非常多的非关键点

但好在，如果我们求出$$u, v$$对应的**管理点**$$u', v'$$
这些非关键点，虽然不存在于虚树中，但是他们**要么被`u‘`管理，要么被`v'`管理**
并且我们只需要求管理点的大小，可以考虑对`sz[子树大小]`操作，并且**树上倍增**，具体来说

![](/media/content_img/virtualTree05.png)

**注意！！！**
第三遍`dfs`的时候维护答案，`dfs(u, v)`只考虑`u <--> v`路径中间**节外生枝**的点，对`u 的管理点 u'`的贡献
而不考虑`v 的子树`，至于`v`的子树什么时候考虑呢？`dfs(v)`的时候再说

### 算法实现
**树上倍增部分**
```bash
    int binLift(int u, int v, const vector<int> &dp, const vector<int> &to) const {
        if (dep[u] > dep[v]) swap(u, v);

if (up[v][0] == u) return 0;

int x = v;
        for (int i = LOG-1; i >= 0; i--) {
            int jump = up[x][i];

if (dep[jump] > dep[u]) {
                int du = dp[u] + abs(dep[jump] - dep[u]);
                int dv = dp[v] + abs(dep[jump] - dep[v]);

if (dv < du or (dv == du and to[v] < to[u])) {
                    x = jump;
                }
            }
        }

return x;
    };
```
**计算部分**
```bash
        auto dfs3 = [&](auto &dfs3, int u, int fa) -> void {
            auto U = to[u];
            ans[U] += tree.sz[u];

for (auto v : adj[u]) {
                if (v == fa) continue;
                ans[U] -= tree.sz[v];
            }

// calc
            for (auto v : adj[u]) {
                if (v == fa) continue;
                if (to[u] == to[v]) continue;

int x = tree.binLift(u, v, dp, to);
                // V:[x -> v], U:[fa[x] -> u];
                if (x == 0) continue;

auto V = to[v];

int delta = tree.sz[x] - tree.sz[v];
                ans[U] -= delta;
                ans[V] += delta;
            }

for (auto v : adj[u]) {
                if (v == fa) continue;
                dfs3(dfs3, v, u);
            }
        };
```
## 树上病毒传播
**[E. Treeland and Viruses](https://codeforces.com/contest/1320/problem/E)**
给定`n`个点的树，`q`个询问，每个询问如下
有`k`种病毒，每种病毒`i = [1, k]`有初次感染的城市`start[i]`，传播速度`speed[i]`
然后给定`m`个关键点，**输出**每个关键点被第几号病毒感染

病毒的传播规则如下
按轮次传播，每一轮病毒`1`先传播，然后是病毒`2`，一直到病毒`k`
下一轮又从病毒`1`开始传播

如果第`i`种病毒已经感染了城市`x`，自己传播时候，想要感染城市`y`，当且仅当
如果城市`x -> y`的路径包含的边数`<= speed[i]`，并且`x -> y`的路径上，除了`x`所有的城市都未被感染
一旦城市被某种病毒感染，就会永久保持，不会再被其他病毒感染，传播一直持续
直到所有城市都被感染，输出给定的`m`个关键点被几号病毒感染

**算法分析**
对每个询问给定`k`，$$\sum k \leqslant 10^5$$，好像可以用多源最短路径？

1）病毒是在树上扩散的，而树中任意两点之间的距离是确定的
所以要用最短路径算法，那也是根据`time[u]`，即`u`这个点第一次被病毒感染的时间
求`time`的最短路径

2）注意到病毒扩散是一轮一轮的，这样就启发我们用**多源最短路 + 根据轮数建立分层图来 dijkstra**
只不过这里分层图相邻两层的间隔不是`1`，需要为每个点添加一个`dist`属性，来维护**这个点到传染源的距离**
从而确定`time = dist / speed`来更新最短路（实际上是最短时间）

> 算法设计，模拟多源 dijkstra 的传染过程即可

对每个节点，`(id, dis, tim, vir)`分别表示`(节点编号，和最近传染源的距离，被感染的时间，被感染的病毒编号)`
用优先队列来维护，优先级设计如下
```bash
先按 tim 排序，tim 越小优先级越高
tim 相等，按病毒编号排序，编号越小优先级越高
```

考虑`dijkstra`的分层扩展，假设`u`这个节点刚刚从优先队列弹出，`(id, dis, tim, vir)`
考虑$$u \to v$$的过程
```bash
disv = dis + |dep(u) - dep(v)|，这是 v 到传染源的距离，是确定的
```
那么令`spd = speed[vir]`表示当前传染源病毒传染速度，病毒从传染源到$$v$$要多长时间呢？
（注意，有可能`v`最后被感染的病毒不是从`u`传过来的，是完全有可能的）
（因为题目中保证了$$u \to v$$之间的城市未被感染，而`u`提前被感染是可以的）

> 什么情况下会发生`u`和`v`感染的不是一种病毒呢？假设说编号`k1, k2`两种病毒
其中`k1`跑的慢，但是离`u`比较近，`k2`跑的快，但是一开始离`u`还比较远
在`u`这个节点，`k2`恰好追上`k1`，然后`k2`继续占领`v`

> 还有什么情况`v`会被**抢占**呢？因为病毒的传播方向不一定都是从上往下
也有可能从下往上，从子树往根，比如优先队列维护的某个病毒，编号`k`很大
它很迟才被弹出，但是**速度非常快**，这样的病毒可以抢占

所以`v`什么时候被感染呢？一定要看**从病毒源到`v`的距离**，而不是只看`(u, v)`距离

那么$$v$$被感染的时间戳是$$timv = \displaystyle \lceil \dfrac{disv}{spd} \rceil$$

然后根据`dijkstra`的逻辑，对每个点维护全局的`time[v], virID[v]`（相当于`dijkstra`的`dis`数组，一开始初始化成$$+\infty$$）
```bash
如果 timv < time[v]，那么 time[v] = timv, virID[v] = vir
如果 timv == tim[v] and vir < virID[v],  virID[v] = vir
```
以上两种情况，把对应的`(idv, disv, time[v], virID[v])`重新放到堆中执行路径松弛即可

### 算法实现
```bash
    auto calc = [&](const vector<int> &ver, const vector<pint> &virus, const vector<int> &city) -> void {
        vt.build(tr, ver);

const auto &mark = vt.mark;
        const auto &adj = vt.adj;

static vector<p64> dp;
        // [min_time, virID]
        dp.resize(n+1);

for (int x : vt.nodes) {
            auto &[mnTime, virID] = dp[x];
            mnTime = inf<i64>, virID = -1;
        }

auto cmp = [](const arr &a, const arr &b) -> bool {
            if (a[2] != b[2]) return a[2] > b[2];
            else return a[3] > b[3];
        };

auto dijkstra = [&]() -> void {
            priority_queue<arr, vector<arr>, decltype(cmp)> heap(cmp);

int id = 0;
            for (const auto &[u, spd] : virus) {
                auto &[mnTime, vir] = dp[u];
                mnTime = 0, vir = id;

heap.push(arr{ u, 0, 0, id });

id++;
            }

while (heap.size()) {
                auto expect = heap.top();
                heap.pop();

auto x = expect[0], disx = expect[1];
                auto exptime = expect[2], expVir = expect[3];
                i64 spd = virus[expVir].second;

if (! (exptime == dp[x].first and expVir == dp[x].second) ) continue;

for (auto y : adj[x]) {
                    i64 toy = disx + 1LL * abs(tr.dep[x] - tr.dep[y]);
                    i64 costTime = (toy + spd - 1) / spd;

auto &[timey, virID] = dp[y];
                    if (costTime < timey or (costTime == timey and expVir < virID)) {
                        timey = costTime, virID = expVir;

heap.push(arr{ y, toy, timey, virID });
                    }
                }
            }
        };

dijkstra();

for (const auto &x : city) {
            cout << dp[x].second + 1 << " ";
        }
        cout << "\n";
    };
```

## 寻宝游戏
**[寻宝游戏](https://www.luogu.com.cn/problem/P3320)**
给定`n`个节点的树，每个节点两种类型，刷宝点和不刷宝的点，树的边有边权
一开始所有的点都是不刷宝的点，给定`m`次操作
```bash
操作 x：x 号点的类型翻转，刷宝的点变成不刷宝的，不刷宝的变成刷宝的
```
一次操作之后，所有刷宝的点都会产生宝物，你需要瞬移到任何点作为出发点（不需要代价）
但是接下来走路要有代价，你需要走路拿到所有的宝物，并且最后回到出发点
输出最小行走路程，`m`次操作每次都要输出

**提示**
树上`k`个节点建立的虚树 = 树上`k`个节点最小连通子树的压缩树

**算法分析**
对这`m`次操作，可以用`set`维护所有的刷宝点，这样就形成了若干个关键点
> 考虑一棵子树，所有的点都要被收集，最少要花费的时间是多少呢？

**最小连通子树的性质**
从任意点出发，走遍树上所有节点，并且最后还要回到出发点，所需要的最小代价是$$2\sum e$$
其中$$\sum e$$表示所有的边权和

从任意点出发，走遍树上所有节点，并且最后**不需要**回到出发点，最小代价是$$(2\sum e) - D$$
其中`D`是**树的直径**

> 那么这个问题的答案就是$$2\sum e$$

现在的问题是，对于每个询问，怎么快速求出**最小连通子树的边权和**
（不可能每一个询问都建出虚树跑一遍，求边权和，太慢了，考虑**怎么根据上一次的答案维护出来**）

那既然答案都是$$2\sum e$$，就说明和起点具体在哪里没有关系，可以考虑排序
这里按照`dfs 序`**从小到大**排序，并选择`dfs 序最小`的作为出发点
```bash
考虑三个点 a, b, c，已经按 dfs 序从小到大排序了
从 a 开始按 dfs 序遍历相邻的点，不难发现

1.  ( b ---> maxdep(lca) ) 这条路径上的点已经被算过 2 次了
2.  如果我们最后让 c ---> a 回到 a 的话，总共 ( c ---> lca ---> a ) 路径上的点也会被算 2 次

归纳一下，可以知道如下结论
```

**新增一个刷宝点`x`**
很简单，找到`x`在`dfn`序中上一个和下一个点`l, r`，`ans`的变化量是
```bash
ans = ans - (l, r) + (l, x) + (x, r)
```
其中$$(l, r)$$表示边$$(l, r)$$的边权，也很容易求，`dep[l] + dep[r] - 2dep[ lca(l, r) ]`

**删除一个刷宝点`x`**
```bash
ans = ans - (l, x) - (x, r) + (l, r)
```
**如果是在最后/最前呢？**
考虑这是一个环形数组，`a[n]`新加进来一个点是`x`，如果`x`被插在最后，对应的`r`应该被视为`a[1]`
最前的情况同理

上述算法，可以用自定义排序规则的`set`很轻松地实现

看完文章有啥想法

算法小站

wiki 主题

数据结构

虚树

目录