wiki - 算法小站

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

字符串

回文串

回文树

[[ item.c ]]

回文串

## 回文串
### 回文串的定义
相关定义
反转串$$S$$，一个字符串$$S = s_1s_2\cdots s_n$$，其反串为
```math
R(S) = s_ns_{n-1}\cdots s_1
```
回文串是满足$$S = R(S)$$的串

**回文中心**
长度是奇数的回文串，回文中心是$$\lceil \dfrac{n}{2} \rceil = \dfrac{n+1}{2}$$（下标从`1`开始）
或者是$$\lfloor \dfrac{n}{2} \rfloor$$，下标从`0`开始

长度是偶数的回文串，回文中心介于$$S(\dfrac{n}{2})$$和$$S(\dfrac{n}{2} + 1)$$之间

**中心扩展法**
枚举回文中心，然后两边扩展，分奇数/偶数讨论
```bash
奇数长度
for i = 1 to n 枚举回文中心 i
	int l = i, r = i;
	while S[l-1] == S[r+1]:
		[l, r] 构成一个回文串
		l---, r++
		
偶数长度
for i = 1 to n, if S[i] == S[i+1]:
	i 才有可能成为回文中心，l = i, r = i + 1
	while S[l] == S[r]:
		[l, r] 构成一个回文串
		l--, r++
```

**回文半径**
回文中心到回文串两端的距离相等，这个距离是回文半径
```bash
a b c b a，回文半径是 3，奇数要包括回文中心
a b c d d c b a，回文半径是 4
```
一个二元组`(回文中心，回文半径)`可以表示回文串

### 回文串的性质
**长度和半径**
**奇回文串**，$$|S| = 2L - 1$$
**偶回文串**，$$|S| = 2L$$
**回文半径的二分性**，回文半径`-1`等价于，同时删掉回文串的首尾字符，依然是回文串
**回文串和 Border**，对于回文串$$S$$，**回文前缀（后缀）**等价于其 Border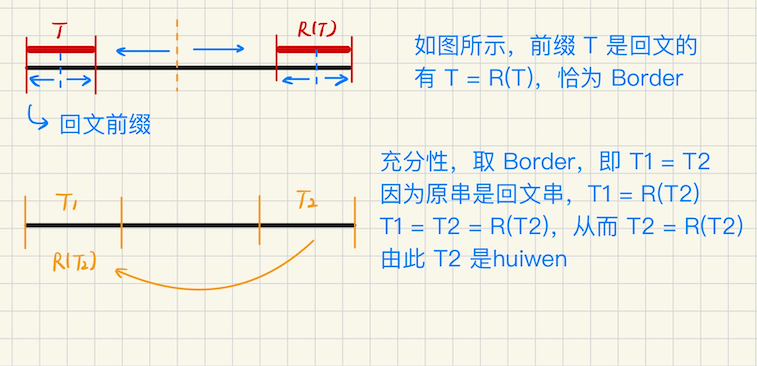
![](/media/content_img/PAMBorder.png)

## Manacher
### 预处理
前期处理，奇偶统一，将$$S$$的每两个字母中间，以及开头结尾插入`#`
```bash
S = bccbeb
S = # b # c # c # b # e # b #
```
这样所有的回文串都变成奇数长度，并且首尾一定是`#`
```bash
原始偶回文串，bccb = # b # c # c # b #,  len = 9，回文中心是 #
原始奇回文串，beb = # b # e # b #，len = 7，回文中心是 e
```
同时，所有极长回文子串的长度一定是奇数，因为极长回文子串一定是以`#`开头和结尾
因为任意两个`#`之间的串的长度，`# ? ? ? #`是奇数

**一些关系**
容易发现，$$|S'|= 2|S| + 1, \quad |S| = \dfrac{|S'| - 1}{2} = \lfloor \dfrac{|S'|}{2} \rfloor$$
此关系对回文半径仍然适用

### 定义
令$$len(i)$$表示以$$i$$为回文中心的最大回文半径
**最右回文串 P：**所有已经求出的回文串中，右端点最靠右的那个

**算法流程**
从左到右求每个位置的回文半径，同时维护最右回文串$$S[L, R]$$以及其回文中心$$p$$
设当前$$1, 2, \cdots i-1$$位置的`len`已经求出来了，当前需要求`len[i]`，根据$$i$$和$$[L, R]$$的关系，分类讨论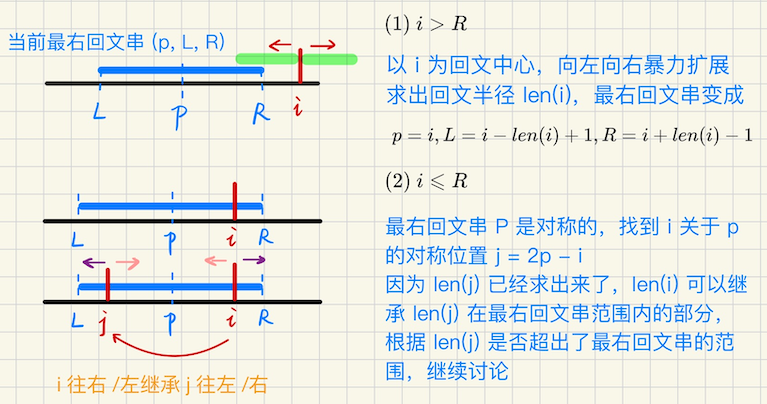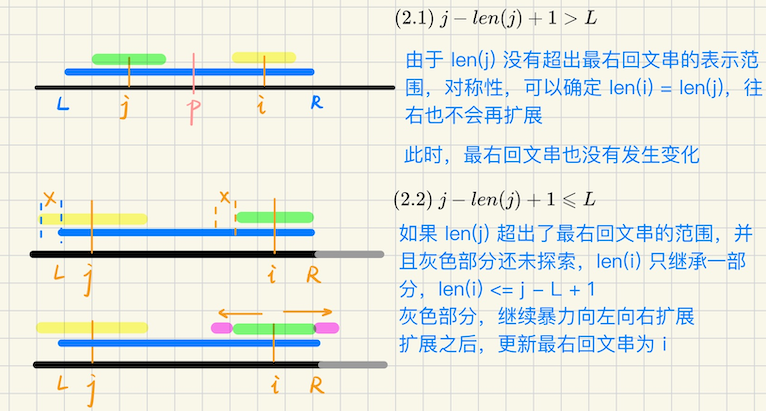

![](/media/content_img/manacher01.png)
![](/media/content_img/manacher02.png)

### 算法实现
```bash
vector<int> manacher(const string &s) {
    string t = "#";
    for (auto c : s) {
        t += c;
        t += '#';
    }
    int n = t.size();
    t = " " + t;

int R = 0, p = 0;
    vector<int> lc(n+1, 0);
    // right-most [.., R) --> check [i, R)
    for (int i = 1; i <= n; i++) {
        if (i < R) lc[i] = min(lc[2*p - i], R - i);
        else lc[R = i] = 1;

while (t[i - lc[i]] == t[i + lc[i]]) lc[i]++;
        if (i + lc[i] > R) R = i + lc[i], p = i;
    }

for (int i = 1; i <= n; i++) lc[i]--;
    return lc;
}
```
说明，算法的最后，对`lc[i]--`，对回文半径进行了`-1`处理，**此时半径是不包括回文中心的**

那么映射到原串的时候，我们有$$\displaystyle |S| = \dfrac{|S'| - 1}{2} = \lfloor \dfrac{|S'|}{2} \rfloor$$，那么我们要求**原串的最长回文子串**
（最后一步成立的原因是，$$|S'|$$长度总是奇数）

对每个位置，manacher 之后的极长回文串就是$$|S'| = 2len(i) + 1$$
对应回**原串**的极长回文串的**长度**就是$$len(i)$$

上述公式对回文半径也成立，manacher 之后求出的回文半径$$|r'| = len(i) + 1$$（包括回文中心）
那么原串的回文半径$$|r| = \lfloor \dfrac{len(i) + 1}{2} \rfloor$$

> 实在不会的时候，画图，考虑`# a # a #`，因为极长回文串，一定是以`#`开头结尾的，为奇数
可知$$|r'| = len(i)+1 = 3$$，对应到原串的半径，应该是$$\lfloor \dfrac{r'}{2} \rfloor = 1$$，恰好符合

### 一些应用
manacher 可以$$O(n)$$求出`len[i]`数组
也就是说，可以求出每个回文中心的回文半径

还可以求**本质不同的回文串**
```bash
abaa
按不同位置开头，一共的回文子串有 {a, aba}, {b} {a, aa} {a}
去重，{a, b, aa, aba} 就是本质不同的回文串
```
在 Manacher 中，新的回文串一定出现在，使得最右回文串右移的时候，因此**本质不同的回文串最多$$n$$个**
把所有更新最右回文串去重，即可得到本质不同的回文串

暴力匹配一步，就有**可能**出现新的回文串，但也有可能这个串已经出现过，都需要纳入考虑
去重可以用哈希

#### 例1
**[如果我让你查回文你还爱我吗](https://ac.nowcoder.com/acm/contest/33548/A)**
给定一个字符串$$S$$，给定`q`个询问，问$$S[L, R]$$有多少个回文子串

> 由于回文串天生的对称性，可以把问题划分成左右两半，$$[l, r]$$分成$$[l, mid] \cup [mid+1, r]$$来思考

预处理阶段，可以先对所有询问离线，并且按照`mid`从小到大的顺序排序
如果回文串的中心在询问区间的左半边，左端点将会限制回文半径的长度，中心在右半边同理
只需要左端点`考虑 j = 1 to mid`做一次，然后对排序的询问`reverse`，`j = N to mid+1`再做一次

实际上，manacher 可以处理出**以$$i$$作为回文中心，极长的回文半径$$r = len(i)$$**
```math
\displaystyle
\begin{cases}
i \leqslant mid \\
i - r + 1 \geqslant L \\
0 \leqslant r \leqslant lc(i)
\end{cases}
```
其中$$mid$$确定，$$i$$是枚举的，$$r$$的取值范围也是确定的，这就是一个二维数点问题
也可以转为线段树

> 考虑用线段树，以回文中心落在左半部分为例

对区间按`mid`从小到大排序，枚举$$j \leqslant mid$$（排序之后，对已经考虑过的`j`不用重复考虑了，`j`实时更新到`mid`）
那么$$[j - lc(j)+1, j]$$都存在合法的回文串，区间修改，`modify(j - lc[j] + 1, j, +1)`

那么对于区间来说，$$[l, r]$$区间内的贡献`+1`，对**实际的回文串个数，增加了多少贡献呢？**
注意到，仅有$$cnt = (r - l + 1) / 2$$个数是有用的，剩下都是`#`

另外，之前马拉车求出的`lc[i]`，回文半径不包括回文中心，线段树区间修改的时候需要特别注意
区间修改对应`[l, r] = [j-(lc[j]+1)+1, j]`，另外只有$$\dfrac{r-l+1}{2}$$个数是有用的，能成为新的回文左端点
这里还需要讨论一下奇偶性，如果$$r - l + 1$$是偶数，那没有问题，如果是奇数呢？
这里不妨记区间有效字符数是`cnt`

形如`# a # a #`肯定没问题，`a # a`，需要`cnt += 1`，也就是说，`[l...r]`的`l`端点是字符而不是`#`的话
需要`+1`，这个怎么判断呢？Manacher 处理后，下标从`1`开始，那么`# a # a ...`，下标在**偶数位置**的一定是字符

最后区间`+1`，不是真的`+1`，而是看看多出了哪些位置能成为新的回文左端点？答案是$$cnt \cdot 1$$

#### 拉拉队排练
**[国家集训队 拉拉队排练](https://ac.nowcoder.com/acm/contest/33548/B)**
给定一个字符串$$S$$，长度是$$1e6$$，求前`K`大的回文子串长度乘积，要求回文串的长度是奇数

**算法分析**
可以用`(回文中心，回文半径)`表示任意的子串，这可以$$O(n)$$用 Manacher 处理出每个位置的$$len(i)$$
之后呢？回文串去掉首尾，子串仍然是回文串，考虑到每个$$i$$
```bash
要么包含奇数长度
2len+1, 2len-1, ...., 3, 1

要么包含偶数长度
2len, 2len-2, ...., 2, 0
```
之前用 Manacher 预处理出来的`lc[i]`数组，是不包括回文中心的，真实回文串的长度是$$2lc(i) + 1$$
对应到**原本**的回文串的长度就是$$lc(i)$$，根据奇偶性分类

可以考虑**一边做一边合并**，用一个计数器`cnt(len)`表示**原串**长度**恰好**是`len`的回文串的个数
```bash
预处理 cnt，因为前 K 大，从大到小考虑

for len = n downto 1, len 为奇数
	let c = min(cnt[len], K)
	长度恰好为 len 的有 c 个，ans *= power(len, c)
	
	cnt[len - 2] += cnt[len],  K -= c
```
注意，这里用到了一个技巧，因为长度更长的回文串，总是包含长度更小的串
所以我们仅考虑长度**恰好是**$$len$$的串，考虑完了之后，$$cnt(len-2) += cnt(len)$$
这样**从大到小**继续考虑$$len - 2$$，不会漏解

#### 最长双回文串
**[国家集训队 最长双回文串](https://ac.nowcoder.com/acm/contest/33548/C)**
给定一个字符串$$S$$，求最长的双回文子串
双回文子串定义为，从一个位置切开，使得前缀和后缀都是回文串，也就是`A + B`拼接
要求`A, B`都是回文串

**算法分析**
很显然的思路，可以枚举分割位置$$i$$，问题转化成，考虑对于$$i$$位置，往左边最长的回文串
以及从$$i+1$$位置，往右边最长的回文串

这个问题，可以转化成**`pos`数组的`min-max`问题**
用线段树维护$$mn[i]$$，表示`i`位置往左边，`[? .... i]`为回文串，最小的`即 most-left`的左端点位置

用 Manacher 求出$$(i, len(i))$$二元组之后，`[L, i] = [i-len[i]+1, i]`（注意，这里的`len`要包括回文中心）

> 但问题来了，线段树怎么更新维护呢？因为$$j \in [L\cdots i]$$**中间仍然是有回文串**的
其中$$[j\cdots i]$$就是一个回文子串，那么对于`[L...j...i]`，`L`可以用来更新$$j$$吗？

答案是不可以的，`[b a .... ] [i] [.... a b]`，此时`b a`并不构成**前缀回文串**，那么怎么进行区间更新呢？
注意到$$[L, l_1, l_2, \cdots i]$$，以这些位置作为回文左端点的回文子串，都有一个**不变的**回文中心
那就是$$i$$，从这里入手考虑

> 算法优化

线段树维护每个位置$$i$$，`mn[i]`表示，以$$i$$作为回文右端点，最左边`most-left`的**回文中心的位置**
同理，`mx[i]`表示以$$i$$作为回文左端点，最右边`most-right`的**回文中心的位置**

这样就可以转移了，拿左半部分来说，对于 Manacher 求出的`(i, len[i])`，其中`len[i]`回文半径的长度要包括回文中心
我们有`[L, i] = [i-len[i]+1, i]`，那么这个区间内，所有的位置，往右找，都可以找到**回文中心`i`**
所以可以用`i`来**对`[L, i]`区间取`max`**，另一半同理

这样，最后的答案是多少呢？枚举分割点$$i$$，考虑`[.... i] and [i+1....]`
右半边，对应的 Manacher 串长度是`(mx - i) * 2 - 1`，而左半边呢，`(i - mn + 1) * 2 - 1`
所以总的回文长度是$$(2(mx-i) - 1) + (2(i-mn+1) - 1) = 2mx - 2mn$$
对应回原串，长度就是`mx - mn`，用来更新`ans`即可

#### ANT-Antisymmetry
**[POI2010 ANT-Antisymmetry](https://ac.nowcoder.com/acm/contest/33548/D)**
给出一个`01`串，求反对称子串的个数
反对称子串定义为，将$$R(T)$$逐位取反后，等于原串$$T$$，则`T`是一个反对称串
比如`0 1 0 1 0 1`，对应`R(T) = 1 0 1 0 1 0`，逐位取反后，`0 1 0 1 0 1`恰好和原串相等

**算法分析**
和 Manacher 本质没有任何不同，原来的 Manacher 暴力扩展的时候，要求两端`t[i - len] == t[i + len]`
在这个问题中，换成`t[i - len] != t[i + len]`，继续扩展即可
`[l+1, r-1] --> [l, r]`能完成扩展的充要条件，是`t[l] ^ t[r] = 1`

```bash
vector<int> manacher(const string &s) {
    string t = "#";
    for (auto c : s) {
        t += c;
        t += '#';
    }
    int n = t.size();
    t = " " + t;

int R = 0, p = 0;
    vector<int> lc(n+1, 0);
    // right-most [.., R) --> check [i, R)
    for (int i = 1; i <= n; i++) {
        if (i < R) lc[i] = min(lc[2*p - i], R - i);
        else lc[R = i] = 0;
		// 注意这里和普通的 Manacher 不同
		// 单个位置，并不是反对称串

while (i - lc[i] >= 1 && i + lc[i] < lc.size() && (t[i - lc[i]] == '#' || t[i - lc[i]] != t[i + lc[i]] ) ) lc[i]++;
        if (i + lc[i] > R) R = i + lc[i], p = i;
    }
	for (int i = 1; i <= n; i++) lc[i]--;
	// 返回的 lc 并不包括回文中心，实际上，[i, i] 也构不成反对称子串
    return lc;
}
```
对于每个位置$$i$$，实际上都有$$\max(0, lc[i])$$种不同的回文半径可以选择
所以答案是$$\sum \max(0, lc_i)$$，但是，有一半的位置是`#`，是无效的，所以`ans /= 2`才是答案

#### 双倍回文
**[SHOI2011 双倍回文](https://ac.nowcoder.com/acm/contest/33548/E)**
给定一个字符串`S`，求最长的双倍回文子串，若一个串能表示成`[T R(T)] [T R(T)]`的形式
那么就是一个双倍回文串，比如`abba abba`，双倍回文串的长度，必须是`4`的倍数
回文一次还不够，要回文`2`次

**算法分析**
注意到，本质不同的回文串，实际上最多只有$$O(n)$$个，所以可以暴力所有的本质不同回文串
然后逐一检查是否是双倍回文

Manacher 算法中，只要发生了**暴力扩展**，那么`lc[i]++`，每`+1`就会产生一个新的本质不同回文串
这里双倍回文怎么办呢？要求原串的回文长度是偶数，很简单，对应的 Manacher 串**回文中心必须是`#`**
当发生扩展的时候，只有`t[i] == #`，才考虑检查并更新

怎么检查呢？
假设说已经找到了回文中心`i`，以及极长回文半径`lc[i]`，考虑**左边一半是不是回文串**
左边一半的回文中心在哪里？假设说一半是`# a #`的回文半径是`3`，`3 / 2 = 1`，回文中心是`a`
回文中心的位置恰好是$$half = i - \dfrac{lc_i}{2}$$

那么做法就比较显然了，对每一个可能发生扩展的位置$$(i, half)$$打表
然后依次检查每一个`j = half`，如果$$j + lc[j] - 1 \geqslant i$$，回文半径超过了`i`
另外还必须满足**偶数**的限制，也就是说`t[j] = #`，此时才满足左半边也是回文串

怎么更新答案呢？`# a #`，此时`j = 1, i = 3`，那么原串中的$$\dfrac{1}{4}$$回文的长度是`(3 - 1) / 2 = 1`（只有一个`a`）

也就是$$(i - j) / 2$$，那么对应原串中的`4`倍回文串长度是$$2(i - j)$$

看完文章有啥想法

算法小站

wiki 主题

字符串

回文串

目录