wiki - 算法小站

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

数据结构

线段树

线段树单点修改

线段树区间修改

动态开点线段树

线段树的合并（一）

可持久化线段树

树链剖分

平衡树

FHQ-Treap

珂朵莉树

分块

位分块

[[ item.c ]]

线段树的合并（一）

## 线段树的分裂和合并
### 线段树的合并
### 基本原理
![](/media/content_img/segtreeMerge.png)

递归合并左右子树，不妨设$$p \leftarrow q$$
如果发现一个节点为空，那么`return 另一个节点编号`，然后回溯出去，这个时候意味着将一整棵子树接在下面

如果两棵树都能够从根节点同时往下走，并且已经走到了叶子结点，那么`add( node[p], node[q] )`
并且**返回`p`（节点编号），回溯回去**

```bash
node[p].l = merge(node[p].l, node[q].l)
node[p].r = merge(node[p].r, node[q].r)
```

递归合并完成之后，记得`pull(p)`，更新一下当前节点

### 模板
这里从一个实际问题入手
**[雨天的尾巴](https://www.luogu.com.cn/problem/P4556)**
给定一个$$n$$个节点的树，每次选择$$(x, y)$$，对`x, y`路径上所有点，发放一袋类型为$$z$$的救济粮
现在问，发放完毕之后，每座房子里最多存放的是哪种救济粮？

**算法分析**
如果只有一种救济粮，那么**树链剖分**，然后对若干段重链区间$$[l, r]$$，差分数组执行`d[l]+1, d[r+1] -1`
最后更新的时候，线段树求出每个点$$x$$的**前缀和**，即`[1...x]`区间和，然后取一个最大值即可

但是这里有多种救济粮，一种比较直接的思路是每个点开一个线段树，然后在$$z$$处单点增加`+1`
最后求出最大值，以及最大值所在的位置，就可以知道是哪种救济粮

但是树链剖分，每个点一个线段树肯定空间难以承受，这里可以考虑将**询问离线**
树链剖分可以求出若干段重链形如`[ l[top(u)]...l[u] ], [l(u)...l(v)]`之类的
那么对于$$(x, y, z)$$，就可以将修改$$z$$**挂载到若干段重链的 dfs 序数组 l[...] 上**

具体地，比如应该执行`[ l[top(u)]...l(u) ]`，令`le = l[top(u)], ri = l(u) + 1`
然后用事件表示
```bash
add(le) = {z1, z2, ..., zm}
del(ri) = {z1, z2, ..., zk}
```
表示在这些位置发生了修改，询问的时候，对于每个节点$$u$$
先令`j = l(u)`，映射到`dfs 序`上，然后看看`j`中有哪些修改，`for zi in add(j)`
然后在**权值线段树**上，单点修改，令`zi += 1`，对于`del(j)`也是类似的，修改完之后再查询

那么最后存放最多的救济粮，就是**权值线段树中，最大值所在的位置**

**注意**，离线把所有的`add, del`操作挂载到相应的节点，然后询问之前，先把节点上挂载的操作结算掉
结算的方法对应线段树的单点/区间修改，然后再在线段树上做查询，这实际上就类似**树上差分的求前缀和**，还原每个点真正的权值
当然，特别注意，这里必须**按照`dfs 序`来做**，才能达到**累加前缀修改**的目的，才能正确求解

> 那么我们讨论线段树合并

如果用树上差分的思想，可以考虑每个点建一棵线段树（一开始每个节点只有根节点）
对于一条路径$$(s, t)$$，线段树维护的是路径上每个节点的**差分值**，也就是单点修改
对$$d(s) + 1, d(t) + 1, d(lca) - 1, d(fa(lca)) - 1$$，发放救济粮`z`，实际上就是
```bash
change(root(s), z, 1), change(root(t), z, 1)
change(root(lca), z, -1), change(root(fa(lca)), z, -1)
```

要求具体的值怎么办呢？实际上就对应子树的权值和，**线段树合并，可以维护子树的权值和**
对于$$u$$的所有儿子$$v$$，全部合并到线段树`root(u)，即 root(u) <-- root(v)`

那么查询呢？实际上是查询最大值，以及最大值出现的位置，这一点在线段树中很容易维护
每一次`merge(x, y, l, r)`之后，**回溯时自底向上**更新每个节点即可

```bash
struct S {
	分别表示救济粮的最大数量，以及最大值出现的位置
	int maxv, pos;
};
```
具体来说，我们在救济粮`z`处单点修改，如果两棵线段树能够走到叶子结点，说明**两个节点有相同类型的救济粮**
两个节点的`maxv`相加，否则的话，合并的两个节点**最多救济粮的类型**一定是不同的，正常线段树节点合并即可

#### 算法实现
```bash
template<class S, S (*op)(S, S)>
class dynamic_Segtree {
public:
    int idx = 1;
    int _n;
    vector<S> a;
    vector<int> ls, rs;

dynamic_Segtree() = default;
    dynamic_Segtree(int n) : _n(n) {
        a = vector<S> (_n<<6, S{});
        ls = vector<int>(_n<<6, 0), rs = vector<int>(_n<<6, 0);
    }
    void New(int &p) {
        if (p == 0) p = idx++;
    }
    constexpr void pull(int p) {
        if (ls[p] && rs[p]) {
            a[p] = op( a[ls[p]], a[rs[p]] );
            return;
        }
        if (ls[p]) a[p] = a[ls[p]];
        if (rs[p]) a[p] = a[rs[p]];
    }

void change(int &p, int l, int r, int pos, int val) {
        if (p == 0) New(p);

if (l == r) {
            a[p].maxv += val, a[p].pos = l;

ls[p] = rs[p] = 0;
            return;
        }
        int mid = (l + r) >> 1;
        if (pos <= mid) change(ls[p], l, mid, pos, val);
        else change(rs[p], mid+1, r, pos, val);

pull(p);
    }

S query(int p, int l, int r, const int ql, const int qr) {
        if (ql <= l && r <= qr) return a[p];
        int mid = (l + r) >> 1;

if (qr <= mid) return query(ls[p], l, mid, ql, qr);
        else if (ql > mid) return query(rs[p], mid+1, r, ql, qr);
        else {
            return op( query(ls[p], l, mid, ql, mid),
                        query(rs[p], mid+1, r, mid+1, qr));
        }
    }
    
    template<S (*f)(S, S)>
    int merge(int x, int y, int l, int r) {
        // x <- y
        if (!x || !y) return x + y;
        if (l == r) {
            a[x] = f(a[x], a[y]);
            return x;
        }

auto mid = (l + r) >> 1;
        ls[x] = merge<f>(ls[x], ls[y], l, mid);
        rs[x] = merge<f>(rs[x], rs[y], mid+1, r);
        pull(x);

return x;
    }
};

struct S {
    int maxv, pos;
};

S op(S a, S b) {
    S res;
    if (a.maxv >= b.maxv) {
        res.maxv = a.maxv, res.pos = a.pos;
    }
    else {
        res.maxv = b.maxv, res.pos = b.pos;
    }
    return res;
}

S f(S a, S b) {
    S res = a;
    res.maxv = a.maxv + b.maxv;
    return res;
}
```
> 具体应用

```bash
void solve() {
    dynamic_Segtree<S, op> tr(N);

vector<int> root(n+5, 0);
    for (int i = 0; i < m; i++) {
        int x, y, z;
        cin >> x >> y >> z;

int lca = hld.LCA(x, y);
        int flca = hld.pa[lca];

tr.change(root[x], 1, tr._n, z, 1);
        tr.change(root[y], 1, tr._n, z, 1);
        tr.change(root[lca], 1, tr._n, z, -1);
        tr.change(root[flca], 1, tr._n, z, -1);
    }

vector<int> ans(n+5, 0);
    auto dfs = [&](auto &dfs, int u, int fa) -> void {
        for (auto v : g[u]) {
            if (v == fa) continue;
            dfs(dfs, v, u);
            root[u] = tr.merge<f>(root[u], root[v], 1, N);
        }
        ans[u] = (tr.a[ root[u] ].maxv == 0) ? 0 : tr.a[ root[u] ].pos;
    };

dfs(dfs, 1, 0);
}
```

## 一些问题
### 天天爱跑步
**[NOIP 2016 提高组 天天爱跑步](https://www.luogu.com.cn/problem/P1600)**
**问题描述**
给定一个$$n$$个节点的树，每个节点$$j$$有一个计数器和权值$$w_j$$，有$$m$$个玩家，每个玩家用$$(s_i, t_i)$$表示
每个玩家都是从`0`时刻开始走，如果玩家在第$$w_j$$时刻恰好经过点$$j$$，那么点$$j$$的计数器值就`+1`
现在问最后每个节点的计数器的值是多少？

**算法分析**
之前用树链剖分 + 动态开点线段树解决了这个问题，这里我们考虑用**树上差分 + 线段树合并**来解决这个问题
和前面分析的一样，对于$$x \to y$$的路径，划分成两部分，$$[x, lca) \cup [y, lca]$$

其中$$[x, lca)$$为上升链，链上所有满足$$dep(i) + w(i) = dep(x)$$的点$$i$$都会`+1`
对每个节点，针对`dep`开一棵线段树，`change(root[x], dep[x], 1)`，`change(root[lca], dep[x], -1)`
实际上就是**点差分**，在$$tr(x)$$对应权值位置`+1`，$$tr(lca)$$对应权值位置`-1`

对于$$[y, lca]$$是下降链，链上所有满足$$w(i) - dep(i) = dep(x) - 2dep(lca)$$的点都会被计数
对每个节点，`change(root[y], dep[x]-2dep[lca], 1), change(root[fa(lca)], dep[x]-2dep[lca], -1)`

值得注意的是，这里$$dep(x) - 2dep(lca)$$可能会$$< 0$$，所以以上统一`dep += n`
```bash
change(root[x], dep[x]+n, 1)，change(root[lca], dep[x]+n, -1)
change(root[y], dep[x]-2dep[lca]+n, 1), change(root[fa(lca)], dep[x]-2dep[lca]+n, -1)
```

> 下面考虑查询

对于每个点$$i$$，上升链和下降链分开统计
```math
\displaystyle
\begin{cases}
dep(i) + w(i) + n = dep(x) + n \\
w(i) - dep(i) + n = dep(x) - 2dep(lca) + n
\end{cases}
```
对于上升链，查询$$? = dep(i) + w(i) + n$$，必须满足$$n+1 \leqslant ? \leqslant N$$
下降链呢，查询$$? = w(i) - dep(i) + n$$，必须满足$$1 \leqslant ? \leqslant N$$
不在对应范围的，直接输出`0`

求每个点$$u$$具体计数器的值，实际上只需要将$$u$$及其子树的线段树，全部**合并到**$$u$$即可
线段树节点信息就是区间和，合并的时候，`a, b`两个节点对应的区间和相加即可

> 特别注意！

上升链和下降链，**权值统计不能混淆**，对每个节点，上升链和下降链**分开统计**
上升链用线段树`root1[u]`维护，下降链用线段树`root2[u]`维护（实际上每个点需要`2`棵线段树）

### Lomsat Gelral
**[Lomsat Gelral](https://codeforces.com/contest/600/problem/E)**
**问题描述**
给定一个$$n$$个节点，根节点为`1`的有根树，每个节点$$i$$有一个颜色$$c_i$$
如果一种颜色在以$$x$$为根的子树中出现次数最多，称其在以$$x$$为根的子树中占**主导地位**
同一棵子树中可能有多种颜色占主导地位，求出以$$x$$为根的子树中，占主导地位的颜色编号和

**算法分析**
之前在 [DSU On Tree](https://www.ringalgo.com/article/9/) 中讨论过这个问题，下面考虑用线段树的合并

很自然地想到，每个节点开一棵线段树，叶子结点表示**颜色$$c$$**，对于每个节点$$u$$
在$$c$$处单点增加`+1`，即`change(root[u], c, 1)`

线段树`maxv`维护颜色**出现次数**最大是多少，`sum`维护出现次数最大的**颜色的编号和**
```bash
if a.maxv > b.maxv:		res.maxv = a.maxv, res.sum = a.sum
if b.maxv > a.maxv:		对称地
if a.maxv == b.maxv:	res.maxv = a.maxv, res.sum = a.sum + b.sum
```

最后考虑节点和节点之间，**线段树的合并**
如果递归到叶子结点，那么说明`tree(a) 和 tree(b)`都含有颜色$$c$$，对于$$c$$这个叶子结点
颜色`c`出现的次数，（若将$$a \leftarrow b$$合并）应该是`a.maxv += b.maxv`
同时呢，叶子结点只有一种颜色，那么出现次数最大的颜色编号和，只有`a.sum = l`
（其中`l = c`，表示叶子结点代表的颜色）

> 算法实现的时候，一边`dfs`一边合并，合并完成之后要及时计算$$u$$的答案
因为和父节点合并之后，这个点的线段树就没有用了，空间会被释放，要及时统计

### 永无乡
**[永无乡](https://www.luogu.com.cn/problem/P3224)**
**问题描述**
有$$n$$座岛屿，每座岛屿$$i$$有一个重要度$$p_i$$（是关于$$n$$的排列），某些岛屿之间有桥，现在有$$2$$种操作
`B x y`表示在岛屿$$x, y$$之间修建新桥
`Q x k`询问当前与岛屿$$x$$连通的所有岛屿中，第$$k$$重要的岛屿（即排名第$$k$$小），输出岛屿**编号**

**算法分析**
查询第$$k$$小，考虑权值线段树，同时需要维护连通性，考虑并查集
并查集还附带有合并操作，可以用**权值线段树的合并**

具体来说，每个点开一棵线段树，线段树的叶子结点是**重要度**$$p_u$$，`change(root[u], p[u], 1)`
另外，还需要找第$$k$$小，需要维护节点出现次数的和`sum`，这样才能在权值线段树上二分
二分找到叶子结点，即重要度$$pi$$之后，输出`ord[pi]`，即返回原本的编号

接着就是合并，同时进行**并查集的合并，线段树的合并**，线段树合并的操作其实比较简单
因为是一个排列，不同的两棵树，是不会递归到同一个叶子结点的，实际上节点合并可以如下定义
```bash
int f(int a, int b) {
	return a + b;
}
a + b 返回的是区间内总共有多少个数
```

最后是询问操作，查询$$x$$连通的第$$k$$小，首先`x = dsu.find(x)`，然后在`root(x)`中查询第$$k$$小

### 更为厉害
**[更为厉害](https://www.luogu.com.cn/problem/P3899)**
给定一棵树，$$a, b$$为`T`中两个不同的节点，如果$$a$$是$$b$$的祖先，我们认为$$a$$比$$b$$更厉害
如果$$a, b$$的距离不超过特定的$$\leqslant x$$，那么就认为$$a, b$$彼此彼此
给定$$q$$个询问，每个询问给定$$p, k$$，问有多少个有序三元组$$(a, b, c)$$满足
```bash
1) a, b, c 是 T 中三个不同的点，并且 a 是 p 号节点
2) a, b 都比 c 更厉害
3) a, b 彼此彼此，这里彼此彼此的常数是 k
```

**算法分析**
对每个询问，$$a$$是确定的，只需要考虑`b, c`，不难发现需要满足以下限制
1）`b`要么是`a`的父亲
2）`b`要么是`a`子树中的点，必须满足$$|dep(b) - dep(a)| \leqslant k$$
3）对应地，`c`就应该是`a, b`中，深度较深的那个点的**后代**（即子树中的点）

> 考虑$$b$$是$$a$$的祖先

首先有$$dep(a) - dep(b) \leqslant k \Rightarrow dep(b) \geqslant dep(a) - k$$
从而$$dep(b) \in [dep(a) - k, dep(a) - 1] = [\max(1, dep(a)-k), dep(a)-1]$$
这里`b`的方案数是固定的，$$(r - l + 1)$$，那么$$c$$呢，$$c$$一定是$$a$$的子树中取一个点
所以$$c$$的方案数是$$sz(a) - 1$$，这部分答案固定，可以直接$$O(1)$$计算
这部分的贡献是$$(sz(a) - 1) \cdot (r - l + 1)$$

> 考虑$$b$$是$$a$$的后代

那么首先$$b$$必须满足$$dep(a)+1 \leqslant dep(b) \leqslant dep(a)+k$$，对于每个这样的$$b$$
能选的$$c$$也一定在$$b$$的子树中
```math
\displaystyle
\sum_{dep_a+1 \leqslant dep_b \leqslant dep_a+k} (sz(b) - 1)
```

只有这部分是需要计算的，直接一边 dfs 一边算是$$O(n^2)$$的

不难发现，这个问题满足
1）`b`在`a`的子树
2）需要对子树中所有满足$$dep \in [dep_a+1, dep_a+k]$$的点，进行贡献$$sz(?) - 1$$的求和

这是一个**子树 + 区间和查询**的问题，可以用线段树合并来求解
每一个点$$b$$，会在$$dep_b$$处产生$$sz(b) - 1$$的贡献，`change(root[b], dep[b], sz[b]-1)`
单点增加即可

然后考虑`a`的时候，把`a`所有的子树`b`中的线段树合并到`root(a)`中，在`root(a)`中查询**区间求和**
```bash
对于线段树
i64 op(i64 a, i64 b) 维护区间和即可

对于节点的合并，i64 f(i64 a, i64 b)
此时说明 a 和 b 在同样的叶子结点，深度都是 dep
那么 a, b 此时维护的是 sz[?] - 1 的和，自然 a <-- b，return a + b
```

> 特别注意

这个问题，在`dfs`递归合并之后，比如`x <-- y`，之后并不意味着$$root(y)$$没有用了
因为后续还有查询，每个查询如果给出$$(y, k)$$，它对我们的答案$$[dep_y+1, dep_y+k]$$是有影响的
所以`root[y]`这棵残缺的树应该得到保留，这可以利用**数组版本的线段树合并**

或者离线处理每个询问，挂载到对应的节点$$y$$上，这样的好处是，可以一边`dfs`一边处理询问
处理完就把对应的子树给释放掉，能够节省一部分空间

### Minimax
**[Minimax](https://www.luogu.com.cn/problem/P5298)**
给定一棵`n`个结点的有根树，根节点是`1`，每个节点**最多**两个子节点，定义`x`的权值如下
如果$$x$$是叶子结点，那么它的权值直接给出，保证叶子结点的权值两两不同
如果$$x$$有子节点，那么它有$$p_x$$的概率权值等于它的子节点权值最大值，有$$1-p_x$$的概率权值等于子节点权值的最小值

现在需要你求，假设`1`号节点的权值有$$m$$种可能性，权值第$$i$$小的权值是$$V_i$$，它的概率为$$D_i$$
```math
\displaystyle
\sum_{i = 1}^{m} i \cdot V_i \cdot D_i^2
```

> 难点在于概率怎么求，先考虑$$O(n^2)$$怎么做

首先肯定离散化，因为叶子结点的权值各不相同，假设离散化之后的权值$$\in [1, N]$$，那么可以
定义$$dp(i, x)$$表示节点$$i$$，取到值$$x$$的概率，那么$$x$$要么从左儿子传过来，要么从右儿子传过来
当然因为节点值各不相同，以下只有一个成立
```math
\displaystyle
dp(i, x) = dp(ls, x) \left( p_i \cdot \sum_{y=1}^{x-1} dp(rs, y) + (1-p_i) \sum_{y=x+1}^{N} dp(rs, y) \right)
```
对称地，对于右儿子的转移，我们也有
```math
\displaystyle
dp(i, x) = dp(rs, x) \left( p_i \cdot \sum_{y=1}^{x-1} dp(ls, y) + (1-p_i) \sum_{y=x+1}^{N}dp(ls, y) \right)
```

> 可以用线段树合并，来维护 dp 值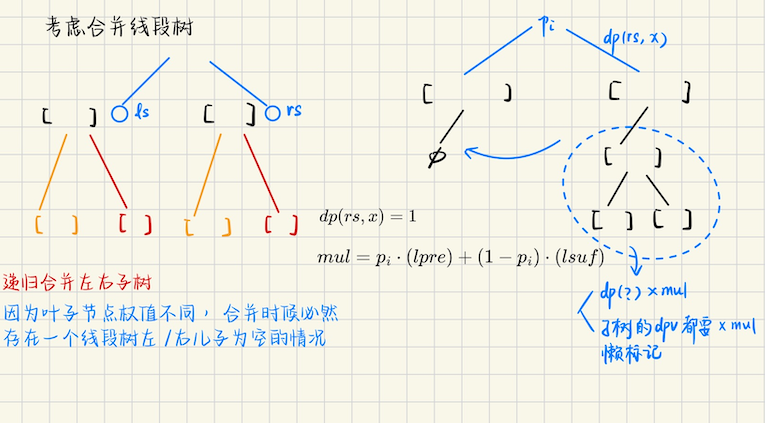

![](/media/content_img/minimax01.png)
![](/media/content_img/minimax02.png)

#### 算法实现
```bash
class dynamic_lazySegtree {
    int merge(int x, int y, mint px, mint sx, mint py, mint sy, mint pi) {
        if (!x && !y) return 0;
        if (!x) {
            mint mul = pi * px + mint(1-pi) * sx;
            a[y] = mapping(mul, a[y], 1, _n), lazy[y] = comp(mul.val(), lazy[y]);
            return y;
        }
        if (!y) {
            mint mul = pi * py + mint(1-pi) * sy;
            a[x] = mapping(mul, a[x], 1, _n), lazy[x] = comp(mul.val(), lazy[x]);
            return x;
        }

push(x, 1, _n), push(y, 1, _n);
        mint lxsum = a[ls[x]], rxsum = a[rs[x]];
        mint lysum = a[ls[y]], rysum = a[rs[y]];

ls[x] = merge(ls[x], ls[y], px, sx+rxsum, py, sy+rysum, pi);
        rs[x] = merge(rs[x], rs[y], px+lxsum, sx, py+lysum, sy, pi);

pull(x);
        return x;
    }
	void dfs(int p, int l, int r, vector<S> &D) {
        if (l >= r) {
            D[l] = a[p];
            return;
        }
        push(p, l, r);
        int mid = (l + r) >> 1;
        dfs(ls[p], l, mid, D);
        dfs(rs[p], mid+1, r, D);
    }
};

void solve() {
    dynamic_lazySegtree<mint, op, int, mapping, comp, id> tr(m);
    vector<int> root(n+1, 0);

auto dfs = [&](auto &dfs, int u, int fa) -> void {
        vector<int> son;
        for (auto v : g[u]) if (v != fa) son.emplace_back(v);

if (son.size() == 0) {
            // u leaf
            tr.change(root[u], 1, tr._n, wgt[u], 1);
            return;
        }
        if (son.size() == 1) {
            dfs(dfs, son[0], u);
            root[u] = root[ son[0] ];
            return;
        }
        for (auto v : son) dfs(dfs, v, u);

root[u] = tr.merge(root[son[0]], root[son[1]], 0,0,0,0, p[u]);
    };
    dfs(dfs, 1, 0);

vector<mint> D(m+5, 0);
    tr.dfs(root[1], 1, tr._n, D);
}
```

> 特别说明，当递归到某个区间$$p$$的时候，$$x, y$$**都存在**
说明左右儿子**都一定能够取到**$$x \in p[l, r]$$区间内的数，$$dp(x)$$当然是`1`，此时直接合并即可

看完文章有啥想法

算法小站

wiki 主题

数据结构

线段树的合并（一）

目录