wiki - 算法小站

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

数据结构

线段树

线段树单点修改

线段树区间修改

动态开点线段树

可持久化线段树

树链剖分

平衡树

FHQ-Treap

珂朵莉树

分块

位分块

[[ item.c ]]

动态开点线段树

## 动态开点线段树
动态开点线段树很重要的一点，就是只把需要用到的点给开出来，其他点不需要去管
具体来说，常常涉及到查询和修改操作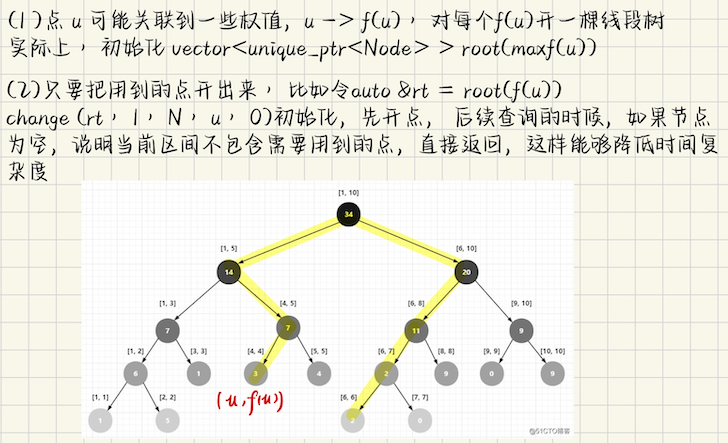

![](/media/content_img/dynSegtree.png)

**先确定查询操作需要用到哪些点**，那么在预处理阶段，可以先把这些点开出来，即从**根到具体的叶子结点的路径**
这样整体的空间是$$O(n \log n)$$的，因为线段树到叶子结点路径上，实际只有$$O(\log n)$$个点

**对于若干修改操作**
如果递归时候遇到空节点，说明**当前区间不包含任何需要用到的点**，直接返回即可

## 一些应用
**[NOIP2016 天天爱跑步](https://www.luogu.com.cn/problem/P1600)**
给定一个$$n$$个节点的树，有$$m$$个玩家，每个玩家都是从`0`时刻出发，沿着路径$$s_i \to t_i$$走
一秒走一条边，现在每个节点有一个计数器，第$$i$$个点有一个权值$$w_i$$，如果玩家在第$$w_i$$秒恰好经过$$i$$
那么计数器会`+1`，现在问最后每个节点的计数器的值是多少

**算法分析**
对于一条路径，不难想到分成上升链$$s \to lca$$和下降链$$lca \to t$$

**上升链**
对于一个节点$$i$$，它什么时候会被观察到呢？当且仅当$$dep(s) - dep(i) = w(i)$$的时候
也就是说，对于一个玩家$$(s, t)$$，**所有满足**$$dep(i) + w(i) = dep(s)$$的，路径$$s \to lca$$上的点
计数器都会`+1`，这个怎么做呢？

这个不难想到，$$s \to lca$$**路径上所有的点**都关联到了$$dep(s)$$，比较无脑的做法是
对**所有可能的`dep`都建一棵线段树**，这样对于一个玩家$$(s, t)$$，只需要在`tr1[ dep(s) ]`上考虑问题
这就简单了，可以用**树链剖分**，剖出$$s \to lca$$上的路径，然后对若干重链`[l...r]`执行**线段树区间加 1**

**下降链**
必须满足$$dep(t) - dep(i) = len - w(i)$$，其中$$len = dep(s) + dep(t) - 2dep(lca)$$
即$$w(i) - dep(i) = dep(s) - 2dep(lca)$$，注意的是这里可能会$$< 0$$，所以我们都`+n`
满足$$w(i) - dep(i) + n = dep(s) - 2dep(lca) + n$$，在`tr2[ dep(s)-2dep(lca)+n ]`上考虑问题

`lca`处增加了`2`次，还需在`tr1[ dep(s) ]`中单点修改，`hld.l[lca]`处减`1`即可
（其中`hld.l[lca]`表示 lca 在 HLD 中的 dfs 序）

**查询**
对于每个节点，上升链中，计数器增加次数是`tr1[ dep(u)+w(u) ]`在`l(u)`处的**单点查询**
下降链中，对应`tr2[ w(u)-dep(u)+n ]`对应`l(u)`处的单点查询，二者加起来即可

**优化**
但是这样还是会 TLE，为什么呢？因为我们没有必要开出那么多点
**只需要关心被查询的点即可**

**对于查询来说**，先预处理，因为只有一部分点是**有效的**，树的深度最大是`n`
如果某些点$$+w_u$$之后，值就$$> n$$了，直接输出`0`，只需要把这些**有效点**先开出来
至于后面的修改，如果递归到某个区间是空节点，说明这个区间不包含任何有效节点
那么自然修改操作无意义，直接`return`即可，这样可以优化很多时间和空间

上升链，**有效**的（即要开线段树的点）节点$$x$$，满足$$1 \leqslant dep(x)+w(x) \leqslant n$$
只在`D = dep(x) + w(x)`落在这个区间的时候，才对相应的`auto &rt = root1[ D ]`建线段树
即`change(rt, 1, n, hld.l[x], 0LL)`，把到$$x$$对应的叶子结点都开出来
如果不在这个区间内，直接输出`0`即可

下降链也是如此，`D = w(x) - hld.dep(x) + n`，落在$$1 \leqslant D \leqslant 2n$$的时候
才应该对`auto &rt = root2[ D ]`建线段树，`change(rt, 1, 2n, hld.l[x], 0LL)`

**接下来修改操作**，对于$$(s, t)$$
若干重链`[l, r]`，令`auto &rt1 = root1[ dep(s) ]`，`tr1.modify(rt1, 1, n, l, r, 1LL, create = false)`
传入`create = false`，表示如果当前节点是`nullptr`，直接返回，不做任何修改，也不需要开多余的节点

对于下降链也是如此，令`auto &rt2 = root2[ dep[s]-2dep[lca]+n ]`，对称地执行操作

**查询的时候**
对于上升链$$D = dep(u) + w(u)$$，如果$$D \notin [1, n]$$，直接输出`0`，否则就正常地在`tr1[ D ]`上
单点查询`l[u]`（`u` HLD 的 dfs 序）的值
对于下降链也是如此

### 算法实现
```bash
class HLD {
public:
    vector<int> dep, pa, hs, sz;
    vector<int> l, r, top, ord;

// idx 是 dfs 序中的元素下标
    int idx = 0;
    int rt = 1;

HLD() = default;
    HLD(int n) 
        : dep(n+1, 0), pa(n+1, 0), hs(n+1, 0), sz(n+1, 0),
            l(n+1, 0), r(n+1, 0), top(n+1, 0), ord(n+1, 0) {
    }

HLD(int _rt, const vector<vector<int> > &G)
        : rt(_rt), dep(G.size(), 0), pa(G.size(), 0), hs(G.size(), 0), sz(G.size(), 0),
            l(G.size(), 0), r(G.size(), 0), top(G.size(), 0), ord(G.size(), 0) {
        dfs1(rt, 0, G);
        dfs2(rt, rt, G);
    };

// 第一遍dfs，求出深度，子树大小，重儿子，父亲
    void dfs1(int u, int fa, const vector<vector<int> > &G) {
        dep[u] = dep[fa] + 1;
        sz[u] = 1;
        pa[u] = fa;
        hs[u] = -1;

for (auto v : G[u]) {
            if (v == fa) continue;
            dfs1(v, u, G);

sz[u] += sz[v];
            if (hs[u] == -1 || sz[v] > sz[ hs[u] ]) {
                hs[u] = v;
            }
        }
    }
    
    // 第二遍dfs，求出dfs序，重链上的链头元素 top[u]
    // 参数 t 是重链的链头元素

void dfs2(int u, int t, const vector<vector<int> > &G) {
        top[u] = t;
        l[u] = ++idx, ord[idx] = u;

if (hs[u] != -1) dfs2(hs[u], t, G);

for (auto v : G[u]) {
            if (v != pa[u] && v != hs[u]) dfs2(v, v, G);
        }

r[u] = idx;
    }

int LCA(int u, int v) {
        while (top[u] != top[v]) {
            if (dep[top[u]] > dep[top[v]]) u = pa[ top[u] ];
            else v = pa[ top[v] ];
        }

if (dep[u] > dep[v]) return v;
        else return u;
    }

using Arr2 = array<int, 2>;
    vector<Arr2> path(int u, int v) {
        vector<Arr2> res;

while (top[u] != top[v]) {
            if (dep[top[u]] > dep[top[v]]) res.push_back({ l[top[u]], l[u] }), u = pa[ top[u] ];
            else res.push_back({ l[top[v]], l[v] }), v = pa[ top[v] ];
        }

if (dep[u] > dep[v]) res.push_back({ l[v], l[u] });
        else res.push_back({ l[u], l[v] });

return res;
    }
};

template<class S, class F>
struct Node {
    S info;
    F lazy;
    unique_ptr<Node> ls = nullptr, rs = nullptr;
};

template<class S, S (*op)(S, S), class F, S (*mapping)(F, S, int, int), F (*comp)(F, F), F (*id)()>
class dynamic_lazySegtree {
public:
    int _n;
    using ptr = unique_ptr<Node<S, F> >;

dynamic_lazySegtree() = default;
    dynamic_lazySegtree(int n) : _n(n) {}

void New(ptr &p) {
        if (!p) p = make_unique<Node<S, F> >();
    }

constexpr void pull(ptr &p) {
        if (p->ls && p->rs) {
            p->info = op( p->ls->info, p->rs->info );
            return;
        }
        if (p->ls) p->info = p->ls->info;
        if (p->rs) p->info = p->rs->info;
    }

void change(ptr &p, int l, int r, int pos, S val) {
        if (!p) New(p);

if (l == r) {
            p->info = val, p->lazy = id();
            return;
        }

int mid = (l + r) >> 1;
        if (pos <= mid) change(p->ls, l, mid, pos, val);
        else change(p->rs, mid+1, r, pos, val);

pull(p);
    }

void push(ptr &p, int l, int r) {
        auto apply = [&](ptr &p, F f, int l, int r) -> void {
            if (f == id()) return;

p->info = mapping(f, p->info, l, r);
            p->lazy = comp(f, p->lazy);
        };

int mid = (l + r) >> 1;
        if (p->ls) apply(p->ls, p->lazy, l, mid);
        if (p->rs) apply(p->rs, p->lazy, mid+1, r);

p->lazy = id();
    }

void push_create(ptr &p, int l, int r) {
        auto apply = [&](ptr &p, F f, int l, int r) -> void {
            if (!p) New(p);
            
            if (f == id()) return;
            p->info = mapping(f, p->info, l, r);
            p->lazy = comp(f, p->lazy);
        };
        
        int mid = (l + r) >> 1;
        apply(p->ls, p->lazy, l, mid);
        apply(p->rs, p->lazy, mid+1, r);

p->lazy = id();
    }

// create true, we use push_create or just create
    // 有时候修改的时候，子节点不存在，不需要新开节点了，状态看作不存在，create = false
    // 有时候修改，子节点不存在要手动开出来，并且将节点值初始化为 S{}, create = true
    void modify(ptr &p, int l, int r, const int ql, const int qr, F f, bool create = true) {
        if (!p && !create) return;

if (ql <= l && r <= qr) {
            p->info = mapping(f, p->info, l, r);
            p->lazy = comp(f, p->lazy);

// 这里看情况，有时候没有懒标记，或者懒标记为 -1 的时候，清空子节点，释放空间, (p->lazy == ?) 看情况写
            if (p->lazy == id()) p->ls = nullptr, p->rs = nullptr;
            return;
        }
        
        create ? push_create(p, l, r) : push(p, l, r);

int mid = (l + r) >> 1;
        if (ql <= mid) modify(p->ls, l, mid, ql, qr, f, create);
        if (qr > mid) modify(p->rs, mid+1, r, ql, qr, f, create);

pull(p);
    }

S query(ptr &p, int l, int r, const int ql, const int qr, bool create = true) {
        if (!p && !create) return S(0);

if (ql <= l && r <= qr) return p->info;
        int mid = (l + r) >> 1;

if (p->info == id()) {
            p->ls = nullptr, p->rs = nullptr;
            return S(0);
        }

create ? push_create(p, l, r) : push(p, l, r);

if (qr <= mid) return query(p->ls, l, mid, ql, qr, create);
        else if (ql > mid) return query(p->rs, mid+1, r, ql, qr, create);
        else {
            return op( query(p->ls, l, mid, ql, mid, create), 
                        query(p->rs, mid+1, r, mid+1, qr, create) );
        }
    }

};

i64 op(i64 a, i64 b) {
    return a + b;
}

i64 id() {
    return 0;
}

i64 comp(i64 f, i64 g) {
    return f + g;
}

i64 mapping(i64 f, i64 x, int l, int r) {
    return x + 1LL * (r-l+1) * f;
}

void solve(int cas) {
    int n, m;
    cin >> n >> m;

int N = 2 * n;

vector<vector<int> > g(n+1);
    for (int i = 0; i < n-1; i++) {
        int x, y;
        cin >> x >> y;
        g[x].emplace_back(y), g[y].emplace_back(x);
    }

vector<i64> w(n+1, 0);
    for (int i = 1; i <= n; i++) cin >> w[i];

HLD hld(1, g);
    dynamic_lazySegtree<i64, op, i64, mapping, comp, id> tr1(n), tr2(N);

using i64node = Node<i64, i64>;
    using ptr = unique_ptr<i64node>;

vector<ptr> root1(n+1);
    vector<ptr> root2(N);

for (int x = 1; x <= n; x++) {
        auto wgt = hld.dep[x] + w[x];
        auto &rt1 = root1[wgt];

if (1 <= wgt && wgt <= n) tr1.change(rt1, 1, tr1._n, hld.l[x], 0LL);
    }

for (int x = 1; x <= n; x++) {
        auto wgt = w[x] - hld.dep[x] + n;
        auto &rt2 = root2[wgt];

if (1 <= wgt && wgt <= N) tr2.change(rt2, 1, tr2._n, hld.l[x], 0LL);
    }

auto upd = [&](int s, int t) -> void {
        auto lca = hld.LCA(s, t);
        auto path1 = hld.path(s, lca), path2 = hld.path(t, lca);
        
        auto &rt1 = root1[ hld.dep[s] ];
        auto &rt2 = root2[ hld.dep[s] - 2*hld.dep[lca] + n ];

for (auto [l, r] : path1) {
            tr1.modify(rt1, 1, tr1._n, l, r, 1LL, false);
        }

for (auto [l, r] : path2) {
            tr2.modify(rt2, 1, tr2._n, l, r, 1LL, false);
        }

tr1.modify(rt1, 1, tr1._n, hld.l[lca], hld.l[lca], -1LL, false);
    };

auto qry1 = [&](int u) -> i64 {
        auto wgt = hld.dep[u] + w[u];
        if (! (1 <= wgt && wgt <= n) ) return 0;

auto res = tr1.query( root1[wgt], 1, tr1._n, hld.l[u], hld.l[u] );
        return res;
    };

auto qry2 = [&](int u) -> i64 {
        auto wgt = w[u] - hld.dep[u] + n;
        if (! (1 <= wgt && wgt <= N) ) return 0;

auto res = tr2.query( root2[wgt], 1, tr2._n, hld.l[u], hld.l[u] );
        return res;
    };

for (int i = 0; i < m; i++) {
        int s, t;
        cin >> s >> t;
        upd(s, t);
    }

for (int u = 1; u <= n; u++) {
        i64 ans = qry1(u);
        ans += qry2(u);

cout << ans << " ";
    }
    cout << "\n";
}
```

看完文章有啥想法

算法小站

wiki 主题

数据结构

动态开点线段树

目录