算法小站
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
登录
注册
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
wiki 主题
算法基础
二维偏序
高维前缀和
搜索
数据结构
线段树
线段树单点修改
线段树区间修改
可持久化线段树
树链剖分
平衡树
FHQ-Treap
珂朵莉树
分块
位分块
字符串
数学
图论
图的连通性
有向图的强连通分量
无向图的割点割边和双连通分量
流和匹配
最大流
最大流的一些应用
图论杂项
最大团搜索算法
树上问题
kruskal重构树
kruskal重构树的一些问题
动态规划
计算几何
杂项
启发式合并
高精度
一些经典问题
约瑟夫环
曼哈顿距离
主题名称
是否为父主题
是否为其添加wiki文章
取 消
确 定
选择主题
修改主题名称
修改父主题
修改wiki文章
取 消
删 除
修 改
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
算法基础
二维偏序
高维前缀和
[[ item.c ]]
0
0
高维前缀和
## 高维前缀和的引入 先回顾一下**二维前缀和**的一种写法 ```bash for i = 1 to n for j = 1 to m sum(i, j) += sum(i, j - 1) for i = 1 to n for j = 1 to m sum(i, j) += sum(i - 1, j) ``` 怎么理解呢?实际上,每一个维度单独考虑,一次只选择一个维度,考虑将$$i-1$$的值合并到$$i$$中 推广到$$n$$维 ```bash for x1 = 1 to n for x2 = 1 to n ... for xk = 1 to n sum(x1, x2, ..., xn) += sum(x1-1, x2, ..., xn) for x1 = 1 to n for x2 = 1 to n ... for xk = 1 to n sum(x1, x2, ..., xn) += sum(x1, x2-1, ..., xn) ...... for x1 = 1 to n for x2 = 1 to n ... for xk = 1 to n sum(x1, x2, ..., xn) += sum(x1, x2, ..., xn-1) ``` ## 解决问题 高维前缀和的核心,在于对于某一个维度,它的值是$$i$$,它不仅包含了$$i$$的信息 还应该包含$$i-1$$的信息 如果对$$i$$从小到大递推,那么$$i$$不仅包含了$$i$$的信息,还应该包含$$\\{0, 1, \cdots, i-1\\}$$的信息 **较小的信息,被包含到较大的信息中去了** 根据这一点,可以这么理解,$$i$$作为下标,$$i \in [0, n]$$,实际上呢,可以用二进制状态压缩 比如说,$$n$$压位成`k`个二进制位,$$n = 2^k - 1$$,那么我们就可以对$$k$$个二进制位单独统计 之前说到,**较小的信息,被较大的信息包含**,可以检查每一个位,`for j = 0 to k`,从**低位到高位** 枚举每一个可能出现的数,`for x = 0 to (1<<k) - 1`,检查第$$j$$位 如果第$$j$$位是`0`,那么它不能再小了,它不包含其他信息 如果第$$j$$位是`1`,那么它不仅应该包含这一位是`1`,还应该包含第$$j$$位是`0`的信息 ```bash 对 K 维前缀和,从低位到高位,一位一位考虑 for j = 0 to K, 考虑每一位,或者说每一个维度 for i = 0 to (1<<K)-1 if (i >> j & 1) dp(i) += dp(i ^ (1<<j)) ``` 进一步地,如果是$$n$$维前缀和,但是**每一位都是`0 or 1`**,也可以用上面的方法求解 ### Dirichlet 前缀和 **[Dirichlet 前缀和](https://www.luogu.com.cn/problem/P5495)** 给定一个长度为$$n$$的序列$$a_1, a_2, \cdots, a_n$$,现在要求一个长度为$$n$$的序列$$b_1, b_2, \cdots, b_n$$,满足 ```math \displaystyle b_k = \sum_{i \mid k} a_i ``` **算法分析** 不难发现,对于每一个$$a_i$$,$$a(i) \xrightarrow{+} a(i \text{ 的倍数})$$ 考虑下标关系,$$id1 = \prod p_i^{\alpha_i}, \quad id2 = \prod p_i^{\beta_i}$$ 当$$a(id1)$$会被加到$$a(id2)$$中,当且仅当$$\beta_i \geqslant \alpha_i$$ 这启发我们用高维前缀和,把每个素数看作一个维度,`for 每个素数` ```bash for 每个素数 p for 每个可能出现的数 i a[i * p] += a[i] ``` 核心在于,把素数看作一个维,$$(i \cdot p)$$应该包含$$i$$的信息 ### Or Plus Max **[E - Or Plus Max](https://atcoder.jp/contests/arc100/tasks/arc100_c)** 给定一个长度为$$2^n$$的序列 ```math a_0, a_1, \cdots, a_{2^n - 1} ``` 对于每一个$$1 \leqslant k \leqslant 2^n - 1$$,求出$$a_i + a_j$$的最大值 其中,$$0 \leqslant i < j \leqslant 2^n - 1$$,另外,$$i \textbf{ or } j \leqslant k$$ **算法分析** 假设没有$$i \oplus j \leqslant k$$的限制,那么把$$N = 2^n - 1$$,压位成关于$$n$$的二进制数 实际上就可以按照之前所说的,用高维前缀和解决,只不过,这里要重载一下求和运算符 求和运算符实际上,是求前缀的**最大值和次大值**,答案就是二者加起来 那么有$$i \textbf{ or } j \leqslant k$$的限制呢? 实际上,就是要求$$i \mid j \leqslant k$$,注意到我们求高维前缀和的时候 从**低位到高位**考虑每一个位,当下标是$$k$$的时候,`k`的某一位假设说是`1`,那么它也包含了这一位是`0`的信息 ```bash 不妨设 k 等于 1 0 0 1 0 1 1 0 1, 它同时包含了下标 ? 0 0 ? 0 ? 0 ? 0 ? 的信息,其中 ?表示这一位既可以是 0 也可以是 1 ``` 每一个$$k$$实际上压了一些状态,它是`1`的位,同时压缩了`(0, 1)`的信息,即$$a(K) = \sum a(\subseteq K)$$ 这里$$\sum$$换成$$\max$$是一样的 值得注意的是,这里不是要求$$k$$的答案,而是$$i \textbf{ or } j = \\{0, 1, 2, \cdots k-1\\}$$这些情况下的$$\max$$ 所以求完高维前缀和数组`a`后,还需要再对`a`求一遍前缀和才是答案 ### Manthan, Codefest 19 **[F. Bits And Pieces](https://codeforces.com/contest/1208/problem/F)** **问题描述** 给定一个长度是$$n$$的序列`a`,现在要求`a[i] | (a[j] & a[k])`的最大值,其中有限制$$i < j < k$$ **算法分析** 考虑枚举$$i$$,从高位到低位,考虑$$x = a_i$$的每一位$$j$$ 如果`a[i] 的第 j 位 = 1`,那么这时候直接令`res |= (1 << j)`,和`ans 取 max` 否则的话,我们要尽可能考虑`a[j] & a[k]`的第`j`位能不能是`1`,这个怎么实现呢? 我们枚举`a[j] & a[k]`所有可能出现的状态`mask`,$$\in [0, 2^{20} - 1]$$,考虑`&`操作合并集合 若某一位为`1`,`mask`集合里的所有数,**这一位都只能是 1** 若某一位是`0`,`mask`集合可以和`这一位是 0 的集合`并,也可以和`这一位是 1 的集合`并 **综上所述,就是`1`中只有`1`,而`0`中可以有`{1, 0}`** 这个就是标准的`SOS dp`,$$dp(1) \xrightarrow{+} dp(0)$$,这里的`+`表示合并操作 这里用`mask`来表示,就是维护所有的`mask` 若`(mask >> j & 1) = 1`,$$dp(mask \oplus (1 \ll j)) \xleftarrow{+} dp(mask)$$(`1`往`0`去并) > 回到问题本身 题目还有限制,就是说$$i < k < j$$,那么很简单,我们`dp[mask] = Info`,`Info`维护`mask`集合中 出现的所有元素,下标的**最大值和次大值** 形式化地说,`mask = {a[?], a[?], ...., a[j], a[k], ...., a[?]}`,`dp[mask] = max{ ?, ?, ..., ?, i, k, ..., ? }` 只要看这个次大值,是否$$> i$$即可 > 算法实现 具体来说,我们尽可能构造`res = a[k] & a[j]`,使得`a[i] | res`尽可能优 如果`a[i] >> j & 1`,那么`res`的第`j`位可以是`0`也可以是`1`,根据前面的讨论,`0 中有 {0, 1}` 所以`res`的第`j`位放`0`,恰好涵盖了这两种情况 否则的话,我们看一下`res`的第`j`位能不能放`1`?`sta = res | (1 << j)`,`dp[sta]`就维护了这种状态 取`dp[sta]`的最大值,次大值`m1, m2`,看一下$$m2 > i$$是否成立?如果成立,`res |= (1 << j)` 否则就不能放`1` 这样我们就尽可能构造了一个最优解了,`chmax(ans, a[i] | res)`即可 ```bash struct Info { int m1, m2; Info &operator+= (const Info &rhs) { Info res; res = *this; auto upd = [&](int val) -> void { if (val > res.m1) { res.m2 = res.m1, res.m1 = val; } else if (val > res.m2) { res.m2 = val; } }; auto [rm1, rm2] = rhs; upd(rm2), upd(rm1); return *this = res; } }; void solve(int cas) { int n; cin >> n; vector<int> a(n+1, 0); for (int i = 1; i <= n; i++) cin >> a[i]; int N = (1<<LOG); vector<Info> dp(N+1, Info{}); for (int i = 1; i <= n; i++) dp[a[i]] += Info{i, 0}; for (int j = 0; j <= LOG; j++) { for (int mask = 0; mask < (1<<LOG); mask++) { if (mask >> j & 1) { dp[mask ^ (1<<j)] += dp[mask]; } } } auto check = [&](const int sta, int i) -> bool { auto [m1, m2] = dp[sta]; return m2 > i; }; int ans = 0; for (int i = 1; i <= n - 2; i++) { int res = 0; auto x = a[i]; for (int j = LOG; j >= 0; j--) { // (a[?] & a[?]) 这一位可以是 1 也可以是 0 if (x >> j & 1) continue; // 否则尽可能让他是 1 int sta = res | (1<<j); if (check(sta, i)) res |= (1 << j); } chmax(ans, a[i] | res); } cout << ans << "\n"; } ``` ### 2025 杭电多校 **[树上 LCM](https://acm.hdu.edu.cn/contest/problem?cid=1172&pid=1007)** 给定一个有$$n$$个节点的树,以及一个数$$x$$,问有多少简单路径的`LCM = x` 路径的`LCM`定义为路径上所有节点的`LCM` **算法分析** 对$$x$$进行素因子分解,不妨设$$p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_k^{\alpha_k}$$ 这些素因子集合假设说是$$P$$ 那对于树上的某个节点`u`,它的权值假设说是`y = a[u]` 对`y`进行素因子分解后,如果出现某个素因子$$p_j \notin P$$,那么`y`无论如何也不可能出现在路径上 如果某个素因子$$p_j^{\beta_j}$$和$$P$$中的$$p_j^{\alpha_j}$$比较,$$\beta_j > \alpha_j$$,这样的点也不可能 先把不可能的点预处理好,记为`sgn[u] = -1` 对$$P$$集合出现的所有素因子进行**状态压缩**,假设$$|P| = m$$,那么`mask in [0, 1<<m)` 如果一个路径的点能取到$$(p_i, \beta_i) = (p_i, \alpha_i)$$,即关于$$p_i$$的幂指能取到$$\alpha_i$$ 那么我们认为在`i`这个位是**满的**,`|= (1 << i)` 路径的`LCM = x`,**当且仅当**路径的状态是`(1<<m) - 1` > 下面考虑怎么实现 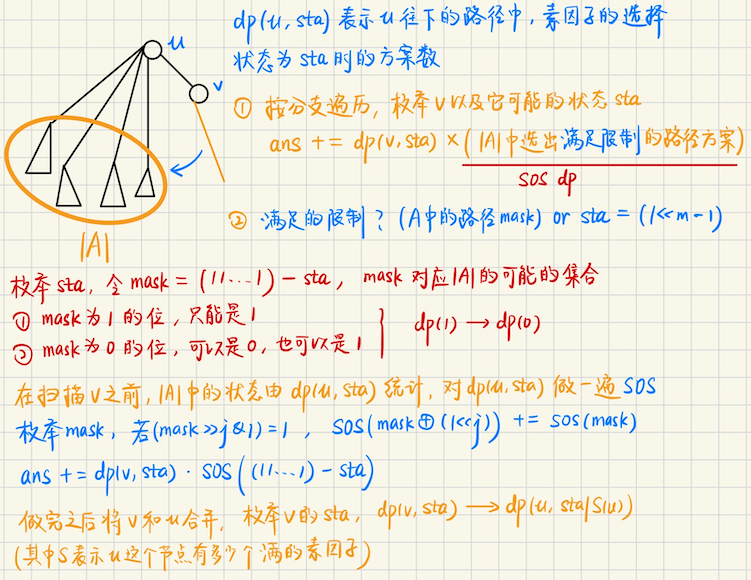 这里$$v$$并到$$u$$的过程,实际上是枚举$$v$$往下的链**能提供的所有素因子状态`sta`** 对应的方案数是`dp(v, sta)`,和$$u$$这个点合并之后,就相当于把这样的链加入集合$$|A|$$中 合并后,`u`能提供的状态就是`(sta | (u 能提供的素因子状态))`,`dp(u, sta | S(u)) += dp(v, sta)` 这样就完成了合并 #### 算法实现 ```bash const int maxn = 1e7; Sieve sieve(maxn); void solve(int cas) { // debug(sieve.primes.size()); int n, x; cin >> n >> x; auto pfac = sieve.factorization(x); vector<vector<int> > g(n+1); for (int i = 0; i < n-1; i++) { int x, y; cin >> x >> y; g[x].emplace_back(y), g[y].emplace_back(x); } vector<i64> a(n+1, 0); for (int i = 1; i <= n; i++) cin >> a[i]; int m = pfac.size(); using pint = pair<int, int>; vector<pint> facs; for (auto [p, num] : pfac) facs.emplace_back(p, num); map<int, int> bits; for (int i = 0; i < m; i++) { auto p = facs[i].first; bits[p] = i; } // debug(bits); // debug(pfac); vector<int> S(n+1, 0); auto div = [&](int u) -> void { auto val = a[u]; // debug(val); bool bad = false; for (auto [p, num] : pfac) { if (bad) break; // if (1LL * p * p > val) break; int cnt = 0; while (val % p == 0) val /= p, cnt++; if (cnt > num) bad = true; if (cnt == num) { auto j = bits[p]; S[u] |= (1 << j); } } if (val > 1) bad = true; if (bad) S[u] = -1; }; for (int u = 1; u <= n; u++) div(u); // debug(S); int ALL = (1 << m) - 1; vector dp(n+1, vector<i64>(ALL + 5, 0)); i64 ans = 0; auto dfs = [&](auto &dfs, int u, int fa) -> void { if (S[u] != -1) dp[u][S[u]]++; if (S[u] == ALL) ans++; for (auto v : g[u]) { if (v == fa) continue; dfs(dfs, v, u); if (S[u] == -1) continue; vector<i64> SOS(ALL+5, 0); for (int sta = 0; sta <= ALL; sta++) SOS[sta] = dp[u][sta]; for (int j = 0; j < m; j++) { for (int sta = 0; sta <= ALL; sta++) { if (sta >> j & 1) SOS[sta ^ (1<<j)] += SOS[sta]; } } for (int vsta = 0; vsta <= ALL; vsta++) { int need = ALL - vsta; i64 res = SOS[need] * 1LL * dp[v][vsta]; ans += res; } for (int vsta = 0; vsta <= ALL; vsta++) { dp[u][vsta | S[u]] += dp[v][vsta]; } } }; dfs(dfs, 1, 0); cout << ans << "\n"; } ```
看完文章有啥想法
发布评论
目录
[[ item.c ]]
29 人参与,0 条评论