wiki - 算法小站

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

图论

图的连通性

有向图的强连通分量

无向图的割点割边和双连通分量

流和匹配

最大流

最大流的一些应用

图论杂项

最大团搜索算法

树上问题

kruskal重构树

[[ item.c ]]

kruskal重构树

## 前置，dfs 序求 lca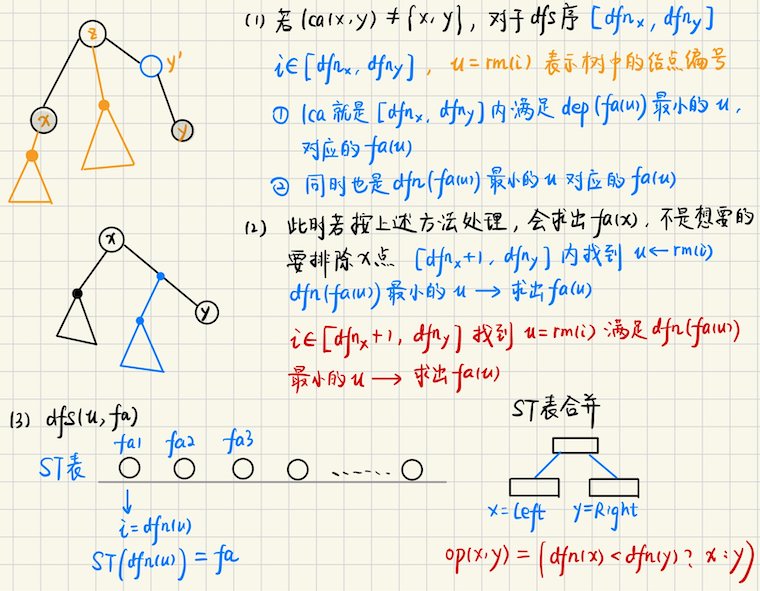
![](/media/content_img/dfsorder-rmq.png)

### 算法实现，RMQ
```bash
// RMQ, 1 index
template<class S, S (*op)(S, S)>
class RMQ {
public:
    vector<vector<S> > f;
    RMQ() = default;

RMQ(const vector<S> &a, int n, int LOG = 20) {
        // a 1 indexed, a[1...n]
        f.resize(n+1);
        for (auto &v : f) v.resize(LOG);

for (int i = 1; i <= n; i++) f[i][0] = a[i];
        for (int j = 1; (1<<j) <= n; j++) {
            for (int i = 1; i + (1<<j) - 1 <= n; i++) {
                f[i][j] = op(f[i][j-1], f[i + (1<<(j-1))][j-1]);
            }
        }
    }

S query(int L, int R) const {
        assert(L <= R);
        int k = topbit(R - L + 1);

while ((1LL<<(k+1)) <= R-L+1) k += 1;

return op(f[L][k], f[R - (1<<k) + 1][k]);
    }
};

vector<int> dfn;
int op(int x, int y) {
    if (dfn[x] < dfn[y]) return x;
    return y;
}
```

### 算法实现，LCA
```bash
void solve(int cas) {
    int n, m, rt;
    cin >> n >> m >> rt;

dfn.assign(n+1, 0);
    vector<vector<int> > g(n+1);

for (int i = 0; i < n-1; i++) {
        int x, y;
        cin >> x >> y;
        g[x].emplace_back(y), g[y].emplace_back(x);
    }

int idx = 0;

vector<int> ST(n+1, 0);
    auto dfs = [&](auto &dfs, int u, int fa) -> void {
        dfn[u] = ++idx, ST[ dfn[u] ] = fa;

for (auto v : g[u]) {
            if (v == fa) continue;
            dfs(dfs, v, u);
        }
    };
    dfs(dfs, rt, 0);

RMQ<int, op> rmq(ST, n);

for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        if (u == v) {
            cout << u << "\n";
            continue;
        }

if (dfn[u] > dfn[v]) swap(u, v);
        auto lca = rmq.query(dfn[u]+1, dfn[v]);
        cout << lca << "\n";
    }
}
```

## kruskal 重构树的构造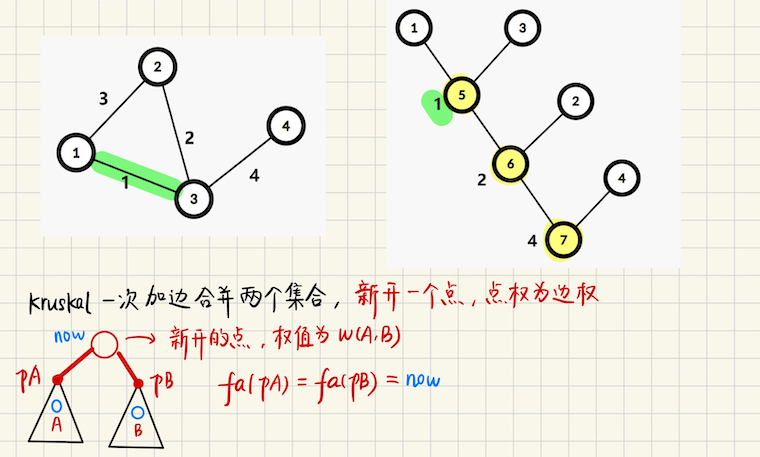
![](/media/content_img/kruskal-tree.png)

新建$$n$$个集合，每个集合恰好有一个节点，点权是`0` ，表示原先图对应的节点

执行 kruskal 算法，每次加边会合并两个集合$$|a|, |b|$$，合并的时候需要如下操作

- 新建一个点`now`，点权是$$w = (a, b)$$，将$$|a|, |b|$$两个集合的 root 置为`now`的左右儿子

- 将两个集合依次合并到新建的点上，新建点设置成为两个集合**新的根**

## kruskal 重构树的性质
**1.**kruskal 重构树是一棵二叉树，节点数为$$2n - 1$$，并且原图中的节点均是重构树中的叶子结点

**2.**对于每个节点，权值$$val$$均大于其子树内任意非叶子结点的权值

**3.**对于原图中任意两个节点$$(u, v)$$，它们之间**简单路径的最大值最小**为$$u, v$$在重构树上 LCA 的权值$$w(lca)$$

> 证明如下
考虑边$$(u, v, w)$$，添加虚点$$(u, v)$$之前，集合$$|U|, |V|$$不连通，因为最小生成树算法
可以知道$$w \geqslant$$`{|U|, |V|集合所有边的边权}`
加入这条边后，`u`经过**这条边**到达`v`就是第一条合法的简单路径，并且之后添加的路径，边权都会比$$w$$更大
所以`LCA`就是**路径最大边权最小的值**

**最小瓶颈路**
定义$$x \to y$$的最小瓶颈路，是$$x \to y$$的所有简单路径中，**最大边权最小的**

**推广性质3**
假设$$r$$是节点$$u$$的某个祖先，那么$$r$$的子树内的所有**叶子结点**$$v$$在原图中，
和$$u$$的最小瓶颈路的权值一定不会超过$$val_r$$

> 常常结合树上倍增一起用，找到一个节点$$val_r > x$$，并且$$r$$的深度尽可能小

> 证明，如果$$u \to v$$没有经过$$r$$，那么`LCA(u, v)`$$\in$$`{r 的子树}`，那么$$val(r) \geqslant val(lca)$$
如果$$(u, v)$$经过$$r$$，那么`LCA`即在$$r$$的子树内，根据**性质3**立刻可得结论成立

看完文章有啥想法

算法小站

wiki 主题

图论

kruskal重构树

目录