wiki - 算法小站

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

图论

图的连通性

有向图的强连通分量

无向图的割点割边和双连通分量

流和匹配

最大流

最大流的一些应用

图论杂项

最大团搜索算法

[[ item.c ]]

最大团搜索算法

**团的问题**
在给定的图中找到团（顶点的子集，都**彼此相邻**，也称为**完全子图**）的计算问题

## 最大团算法思想
**递归和回溯**
1）维护当前的最大团，每次加一个点进来，检查这些点是不是仍然在一个团中。如果加点之后，不是一个团了
那么回溯到满足条件的位置，加入别的点

2）在实现过程中，我们并不知道某个顶点$$v$$**最终**是不是最大团的点，如果递归算法选择到了$$v$$作为最大团成员时，
没有找到最大团，那么应该回溯，把$$v$$ pop 掉，然后尝试查找包含其他点的最大团

3）最大团问题是 **NP-Complete** 的，目前有$$O(3^{n/3})$$指数时间复杂度的算法，以及近似算法

## Bron-Kerbosch 算法
定义三个给定的集合$$R, P, X$$递归搜索
$$R$$集合表示当前极大团中已经加入的点
$$P$$集合表示极大团中还可能加入的点（即扩张极大团，这些点和$$R$$中的点都是有边相连的）
$$X$$集合记录已经被选过的点，作用是判重，同时也是可以用来回溯的

**优化的 Bron-Kerbosch 算法**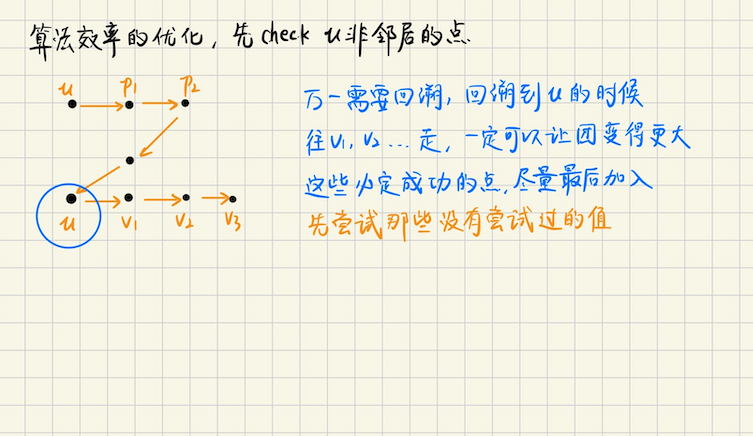
![](/media/content_img/maxclique01.png)
![](/media/content_img/maxclique02.png)

1）初始化$$R, X$$集合为$$\emptyset$$，集合$$P$$是图中所有顶点的集合，$$R$$为已经选出的极大团
2）尝试扩展极大团$$R$$，选取一个顶点，怎么选呢？
选取位于$$P \cup X$$中的一个点$$u$$作为 **pivot**
接着取和$$u$$**不相邻的点**$$v$$，$$R := R \cup \\{v\\}$$

> 如果$$u$$能够被选为最大团，那么$$u$$的邻居$$adj(u)$$也一定可以被选择
那么我们应该优先**给其他点机会**，看看能不能形成更大的团，如果不行了，
迫不得已，就再回溯到$$u$$，把$$adj(u) = \\{v_1, v_2, \cdots \\}$$都选上
这样可以避免错误选择，导致回溯开销过大

> 一旦确定了$$u$$在**最终的最大团中**，$$v_1, v_2, \cdots$$都可以被选进去，不会被回溯
所以这些邻居应该最后被考虑（把机会让给别人）

3）把$$v$$选入最大团，$$\textbf{dfs}(R \cup \\{v\\}, P \cap adj_v, X \cap adj_v)$$
同时$$P := P -\\{v\\}, X:= X \cup \\{v\\}$$

### Codeforces Round 533
**[E. Helping Hiasat](https://codeforces.com/contest/1105/problem/E)**
**问题描述**
给定一个时间轴，每一个时间轴有两种操作，`1`表示 Hiasat 可以改变他的用户名，`2 s`表示用户`s`来访问 Hiasat 的主页
如果`s`发现此时主页的用户名恰好也是`s`，那么`s`会成为好朋友，现在问最多有多少个好朋友

**算法分析**
先考虑每一个`1`操作，为每个`1`操作编号，两个`1`之间出现的人是$$s_1, s_2, \cdots, s_k$$
这些人都是**冲突**的，只能选一个，这像不像独立集？

一个结论是，**图的最大独立集 = 补图的最大团**

那么考虑建图，这种问题一般需要维护**候选点集合**$$S$$，考虑$$n+1$$次操作
当`操作类型 = 1`，或者是操作次数$$> n$$时，根据**候选点集**来建图，同时`clear()`候选集合
当操作类型$$\neq 1$$的时候，把相应的点加入候选集合，候选集合的点是**两两冲突**的

> 怎么建图呢？
暴力即可，$$\textbf{for } x, y \in S$$，`g[x][y] = g[y][x] = 1`

然后对`g`取反，这样就求出了补图，求这个补图的最大团即可

**算法实现**
#### Bron-Kerbosch  算法
```bash
void solve() {
    int ans = 0;
    auto dfs = [&](this auto &&self, const int n, i64 R, i64 P, i64 X) -> void {
        // vertex: [1...n]
        // P vertex can be chosen as max clique
        // X vertex has been done, use for back trace
        // R the max clique now
        if (P == 0LL && X == 0LL) {
            int res = popcnt(R);
            chmax(ans, res);
            return;
        }

int u = 0;
        while ( !( (P|X) >> u & 1) ) u++;

for (int v = 1; v <= n; v++) {
            if ((P >> v & 1) && !(adj[u] >> v & 1)) {
                self(n, R | (1LL << v), P & adj[v], X & adj[v]);
                P -= (1LL << v), X |= (1LL << v);
            }
        }
    };

auto maxclique = [&]() -> void {
        i64 P0 = (1LL << (m+1)) - 2;
        dfs(idx, 0, P0, 0);
    };

maxclique();
    cout << ans << "\n";
}
```
#### 建图参考
```bash
void build() {
    int n, m;
    cin >> n >> m;

vector g(m+5, vector<int>(m+5, 0));
    
    int j = 0, idx = 0;
    map<string, int> id;
    set<int> st;

for (int i = 1; i <= n+1; i++) {
        int op;
        if (i <= n) cin >> op;

if (op == 1 || i > n) {
            for (auto x : st) for (auto y : st) g[x][y] = g[y][x] = 1;
            st.clear();
        }
        else if (i <= n) {
            string str;
            cin >> str;

int k = (id.contains(str) ? id[str] : id[str] = ++idx);
            st.insert(k);
        }
    }

for (int a = 1; a <= m; a++) {
        for (int b = 1; b <= m; b++) {
            g[a][b] = !g[a][b];
        }
    }
    
    vector<i64> adj(idx+5, 0);
    for (int x = 1; x <= m; x++) {
        for (int y = 1; y <= m; y++) {
            if (!g[x][y]) continue;

adj[x] |= (1LL << y);
        }
    }
}
```
## 最大团启发式算法
### 染色规则
记$$R$$是候选点集，$$C_k = \\{v_1, v_2, \cdots\\}$$表示染成颜色$$k$$的所有点的集合
对候选点集$$R$$中的顶点逐一染色，每个顶点$$v \in R$$被插入到**颜色集合**$$C_k$$中，
其中$$C_k$$**满足点集内所有的顶点均和$$v$$不相邻**，令$$C_k \leftarrow v$$
（如果当前所有的颜色类中，都有和$$v$$相邻的顶点，开一个新的颜色类）

颜色类的数量即为$$R$$的诱导子图中，最大团大小的上界，颜色类数量越少，上界越紧（接近真实最大团的大小）

### 原始算法
不难发现，颜色集合**编号**越大，意味着从其中的点出发，更有可能找到**更大的团**
贪心地，可以从颜色编号尽可能大的点出发去寻找最大团

贪心地，我们从$$C_k$$中找到一个点$$p$$，从这个点$$p$$出发寻找最大团，当然这里可以考虑剪枝
如果$$p$$的颜色编号是$$C(p)$$

假设当前维护的极大团是$$Q$$，而当前的最大团是$$Q\_{\max}$$
当且仅当$$|Q| + C(p) > |Q\_{\max}|$$的时候，才考虑递归下去寻找

```bash
R: 当前的候选节点
C: 节点的颜色
Q: 当前维护的最大团

MaxClique(R, C)
	while R != empty() 非空 do
		从候选节点集合 R 中，选择一个拥有最大颜色编号 C(p) 的点 p
		R := R - {p}
		
		if |Q| + C(p) > |Qmax| then
			Q := Q + {p}，尝试加入
			
			if R and adj(p) != empty()，检查 p 还未被选择的邻接顶点，then
				重新计算节点颜色集，from G(R and adj(p))，得到 C2
				MaxClique(R and adj(p), C2)
			else if |Q| > |Qmax|，then Qmax := Q
 		
			Q := Q - {p}，回溯
```

### ColorSort
朴素算法中，按照颜色编号排序，然后依次加入$$|Q|$$中，这样其实效率并不高。
因为从颜色编号最大的点，搜索到最大团的中心节点，有可能还需要很多个步骤，
而度数最大的点，则更有可能成为最大团的中心节点

注意到，对于颜色$$C(v) < |Q\_{\max}| - |Q| + 1$$的顶点$$v \in R$$，**无需按颜色排序**
因为此时 MaxClique 算法不会将这些顶点添加到当前团$$Q$$中

我们检查一个点的颜色编号$$C(v) = k$$，$$[1\cdots kmin-1]$$这部分的点，按**顶点度数排序**，放到候选集合中
其他的点$$[kmin, \cdots)$$按**颜色编号类递增**的顺序，从颜色类$$C_k$$按索引递增的顺序，复制到候选集合中

**最终顺序**
新的候选集合$$T$$，前端的颜色是$$< k\_{\min}$$，并且保持度数非递增（$$\geqslant$$）
而颜色编号$$\geqslant k\_{\min}$$，按照颜色类编号顺序排序

实际上，我们要求$$k \geqslant |Q\_{\max}| - |Q| + 1$$，而$$|Q\_{\max}| - |Q| \geqslant 1$$才有意义
也就是说，至少$$k \geqslant 2$$，颜色类前半段按度数，后半段按颜色编号的情况，只有在$$k \geqslant 3$$才会发生

```bash
ColorSort(R, C)
	从当前的候选点集 R 的最后一个元素开始扩张，获取下一个候选点集 T
	for (auto v : Vertex) if ( g[R.back()][v] ) T.push_back(v)
	
	j = 0, mxk = 1, mnk = max(1, |Qmax| - |Q| + 1)
	C[1].clear(), C[2].clear()，最早的两个颜色类不要了
	
	for v in T:
		k = 1, while (C[k] and v) == empty(), k++，k 是第一个有 v 相邻顶点的颜色类
		if (k > mxk) maxk = k, C[maxk + 1].clear()，新开一个颜色类来放
		if (k < mnk) T[j++] = {v}
		C[k].push_back(v)
		
	if (j > 0) T[j-1] = 0
	for (k = [mnk ... mxk]) for (all u in C[k])  T[j].v = v, T[j++].color = k
	
	ColorSort(T, C)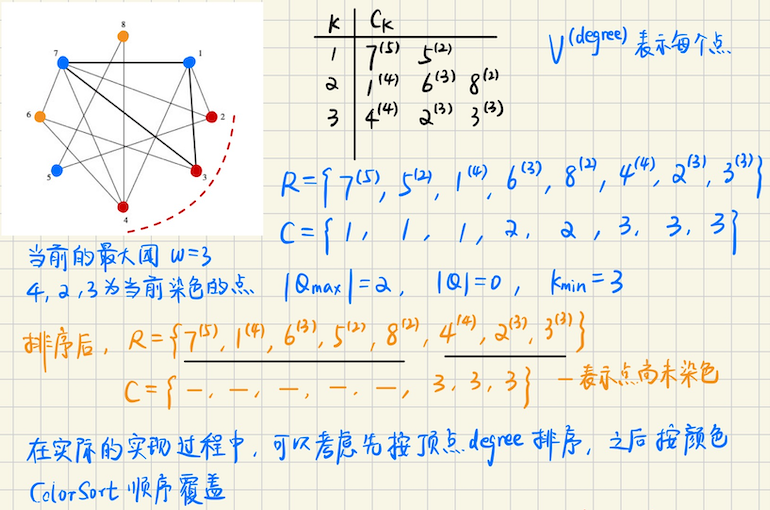
```
![](/media/content_img/maxclique03.png)
![](/media/content_img/maxclique04.png)

### 启发式搜索剪枝
在候选点集$$R$$足够大的时候，通过按顶点在诱导子图$$G(R)$$中的度数进行排序，才可以实现性能的提升
MaxClique 算法的初始层级，$$R$$的规模更大，而递归深度逐渐加深，层级就减小，$$|R|$$也逐渐变小

> 较大的候选点集，计算更紧上界的开销，远小于应用轻松上界的时候，因为错误探索回溯造成的开销
而对于较小的候选点集而言，搜索错误就及时回溯调整就好了，多几次错误冗余搜索，也不会影响性能

定义$$T(level)$$表示截至当前层级的步骤数，占已完成所有步骤数的比例
```math
\displaystyle
T(level) = \dfrac{S(level)}{AllSteps}
```
其中$$AllSteps$$是一个全局步骤计数器，在 MaxCliqueDyn 算法的每一步都会`+1`，同时引入$$T\_{lim} = 0.025$$的参数

当$$T(level) < T\_{lim}$$的时候，需要执行 ColorSort，对$$< kmin$$的节点，执行**按度数递减排序**
当$$T(level) \geqslant T\_{lim}$$的时候，不执行额外的 ColorSort

![](/media/content_img/maxclique05.png)

> 需要关注的是，从上一次到$$level$$，然后又回溯到$$level$$，中间经历了几步？

```math
\displaystyle
S(level) := S(level) + (S(level - 1) - S_{old}(level) ) \\
S_{old}(level) := S(level - 1)
```
> 其实结合递归图不难理解，$$S\_{old}(level)$$相当于$$(l, r]$$的左区间，求前缀和的时候
需要开区间，所以$$S\_{old}(level) := S(level - 1)$$

**算法描述**
```bash
维护一个全局的颜色集合 C[1...k]，C[k] = { 染色成 k 的顶点 }
R：候选点集
lev：递归层数

expand(R, lev = 1)
	S[lev] += S[lev - 1] + old[lev]
	old[lev] = S[lev - 1]
	
	while R is not empty()
		u := 顶点颜色编号最大的候选集的点，实际上就是 R.back
		Q := Q + { R.back() }
		
		尝试从 R.back() 处开始扩张，看看有没有新点加入 |Q|，计算新的候选点集 T
		for v in R, if g[R.back()][v], then T := T + {v}
		
		if T is not empty():
			if (S[lev]++ / ++all < lim) ColorSort(T)，部分前面的点进行度数排序
			
			为新加入的点染色，并且更新颜色集合，把 >= kmin 的点，按颜色编号顺序插入 T
			
			j = 0, mnk = 1, mxk = max(|Qmax| - |Q| + 1, 1)
			C[1].clear(), C[2].clear()
			
			for v in T:
				k = 1, while (C[k] and v) == empty(), k++，k 是第一个有 v 相邻顶点的颜色类
				if (k > mxk) maxk = k, C[maxk + 1].clear()，新开一个颜色类来放
				if (k < mnk) T[j++] = {v}
				C[k].push_back(v)
			if j > 0, T[j - 1].d = 0 (因为每次从 R 最末尾开始扩张，只需要将 j-1 位置去色即可)
			
			此时具有颜色 k = [mnk, mxk] 的所有点，按颜色编号排序，顺序插入 T 中
			for k = [mnk...mxk] for nd in C[k]:
				T[j].v = nd, T[j++].d = k
				
			expand(T,  lev + 1)
		
		else if |Q| > |Qmax|, then Qmax = Q
		
		Q := Q - { Q.back() }，回溯
		R := R - { R.back() }
```

### ICPC-world-finals 2014
**[Sensor Network](https://open.kattis.com/problems/sensor)**
**问题描述**
给定二维平面的点集，每个点集都是传感器，需要挑出最多的传感器，使得两两之间的欧几里得距离$$\leqslant d$$

**算法分析**
遍历传感器，如果$$dist(x, y) \leqslant d$$，那么$$x, y$$连无向边
求出图的最大团即可

#### 算法实现
**最大团启发式搜索**
```bash
const int N = 105;
using graph = vector<bitset<N> >;

class MaxClique {
public:
    double lim = 0.025, steps = 0;

struct Vertex { int v, d = 0; };
    using vv = vector<Vertex>;

graph g;
    vv V;
    vector<vector<int> > C;
    vector<int> qmax, q, S, old;

void init(vv &R) {
        for (auto &x : R) x.d = 0;
        for (auto &x : R) for (auto y : R) x.d += g[x.v][y.v];
        sort(R.begin(), R.end(), [&](const auto &a, const auto &b) {
            return a.d > b.d;
        });

int mxD = R[0].d;
        for (int i = 0; i < R.size(); i++) R[i].d = min(i, mxD) + 1;
    }

MaxClique() = default;
    MaxClique(graph _g) : g(_g), C(_g.size() + 1), S(C.size()), old(S) {
        for (int i = 0; i < g.size(); i++) V.push_back({i});
    }

void expand(vv &R, int lev = 1) {
        S[lev] += S[lev-1] - old[lev];
        old[lev] = S[lev-1];

while (R.size()) {
            if (q.size() + R.back().d <= qmax.size()) return;

q.push_back(R.back().v);
            vv T;
            for (auto y : R) if (g[R.back().v][y.v]) T.push_back({y.v});

if (T.size()) {
                // ColorSort for T
                if (S[lev]++ / ++steps < lim) init(T);
                int j = 0, mxk = 1, mnk = max( 1, (int)(qmax.size()-q.size()+1) );
                C[1].clear(), C[2].clear();

for (auto y : T) {
                    // try to add y to max clique, and maintain color set C[k]
                    int k = 1;
                    auto f = [&](int item) { return g[y.v][item]; };
                    while (any_of(C[k].begin(), C[k].end(), f)) k++;

if (k > mxk) mxk = k, C[mxk+1].clear();
                    if (k < mnk) T[j++].v = y.v;

C[k].push_back(y.v);
                }
                if (j > 0) T[j-1].d = 0;
                for (int k = mnk; k <= mxk; k++) for (auto x : C[k]) {
                    T[j].v = x, T[j++].d = k;
                }

expand(T, lev + 1);
            }
            else if (q.size() > qmax.size()) qmax = q;

q.pop_back(), R.pop_back();
        }
    }

// after expand, qmax is the max-clique
    vector<int> getmax() {
        // return max-clique
        init(V), expand(V);
        return qmax;
    }
};
```
**建图，实现算法**
```bash
using arr = array<int, 2>;

void solve(int cas) {
    int n, D;
    cin >> n >> D;
    
    vector<arr> a(n);
    for (int i = 0; i < n; i++) cin >> a[i][0] >> a[i][1];

graph g(n);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (i == j) continue;

auto [x1, y1] = a[i];
            auto [x2, y2] = a[j];

int dis = 1LL * (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2);
            if (dis <= D * D) g[i][j] = 1;
        }
    }

// finding MaxClique
    MaxClique G(g);
    auto clique = G.getmax();

cout << clique.size() << "\n";
    for (auto x : clique) {
        cout << x + 1 << " ";
    }
    cout << "\n";
}
```

看完文章有啥想法

算法小站

wiki 主题

图论

最大团搜索算法

目录