2026年二月算法竞赛选题（一）

[[ slider_text ]]

[[ item.c ]]

2026年二月算法竞赛选题（一）

发布时间 2026-02-14 作者：zhangminchen 来源：算法小站

构造

## Educational Codeforces Round 163
### F
**[F. Rare Coins](https://codeforces.com/problemset/problem/1948/F)**
有`n`个袋子，第`i`个袋子中有$$a_i$$个金币和$$b_i$$个银币
每个金币的价值是`1`，每个银币的价值独立地是`0 or 1`，是`0`的概率是`1/2`，是`1`的概率也是`1/2`
独立回答`q`个询问
`l, r`，计算`[l, r]`袋子中硬币总价值严格大于其他所有袋子硬币总价值的概率

**算法分析**
不妨设`[l, r]`区域为`A`，剩下的区域是`B`，假设说金币数量记为$$G_A,G_B$$
银币的数量记为$$S_A, S_B$$，那么当且仅当$$G_A + S_A > G_B + S_B$$才满足条件

其中$$G_A, G_B$$的数量是确定的，不妨记$$c = G_B - G_A$$，那么问题的答案是$$\displaystyle\dfrac{S_A - S_B > c \text{ 的方案数}}{2^{\sum b}}$$

> 下面考虑怎么求$$S_A - S_B > G_B - G_A$$的方案数，下面令区域`A, B`**总的银币数量**分别是$$S_A, S_B$$
选出有效的银币数量是$$i, j$$

考虑暴力枚举选了几个有效的（计分的）`B`
```math
\displaystyle
\sum_{i} \binom{S_A}{i} \sum_{i - j > G_B - G_A} \binom{S_B}{j}
```
有点像**范德蒙卷积**，考虑枚举$$d = i - j > G_B - G_A$$，那么$$i = j + d$$
```math
\displaystyle
\sum_{d > G_B - G_A} \sum_j\binom{S_A}{j+d} \binom{S_B}{j} = \sum_{d > G_B - G_A} \sum_j\binom{S_A}{j+d} \binom{S_B}{S_B - j} 
```
可以用范德蒙卷积了
```math
\displaystyle
\sum_{d > G_B - G_A} \binom{S_A + S_B}{S_B + d}
```
而$$S_A, S_B$$是确定的，那么要考虑$$k = S_B + d$$，并且$$k \in [G_B-G_A+S_B+1, S_A+S_B]$$

答案是$$\displaystyle \sum_k \binom{S_A + S_B}{k}$$，再除以$$2^{\sum b}$$

两部分都可以前缀和求解

## Codeforces Round 890
### C
**[To Become Max](https://codeforces.com/contest/1856/problem/C)**
给定一个序列`a[1...n]`，每次可以选择一个下标，满足$$1 \leqslant i \leqslant n-1$$，并且$$a\_{i} \leqslant a\_{i+1}$$
执行`a[i] += 1`，问最多进行`K`次操作之后，序列的最大值

**算法分析**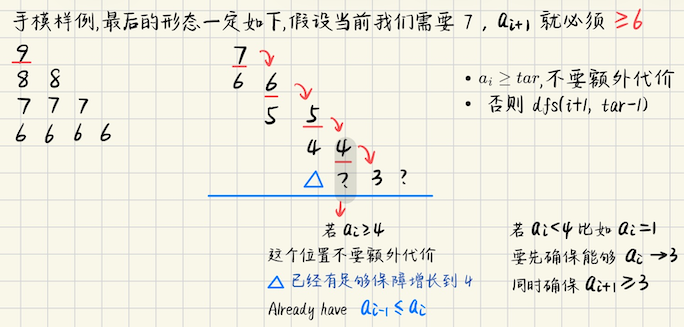
![](/media/content_img/cf890C.png)
```bash
auto dfs = [&](this auto &&self, int i, int tar) -> int {
    if (a[i] >= tar) return 0;
    if (i == n) {
        return tar == a[i] ? 0 : -1;
    }
    int dpv = self(i+1, tar-1);
	
    if (dpv > K or dpv == -1) return -1;
    else return dpv + tar - a[i];
};
```
对每个位置，二分想改成的数`tar`，用`dfs`来判定`tar`是否合法即可

## Codeforces Round 887 (Div. 1)
### B
**[B. Imbalanced Arrays](https://codeforces.com/contest/1852/problem/B)**
构造题，给定一个序列`a`，称一个长度是`n`的序列是**不平衡数组**，当且仅当
1)$$-n \leqslant b_i \leqslant n, b_i \neq 0$$
2)不存在两个下标$$(i, j)$$，使得$$b_i + b_j = 0$$
3)对于每个$$1 \leqslant i \leqslant n$$，恰好有$$a_i$$个下标$$1 \leqslant j \leqslant n$$使得$$b_i + b_j > 0$$
其中$$i, j$$可以是一样的，构造`b`，或者判断不可能

**算法分析**
不难发现，所有填上正数的位置，**构成了一个团**，而所有填上负数的位置，构成一个**独立集**
并且有一个贪心，`deg`越大的数，越有可能在团中，`deg`越小的数，越有可能在独立集中

团的问题是`NP-hard`的，没有多项式时间的解，这里我们并不能一开始就确定团的大小
只能考虑边做边加入团，**动态扩张团**

> 怎么做呢？突破口在`n`，有`n`个点，填上绝对值`[1...n]`，不难发现可以从**排列入手**
`n`次迭代，每次迭代安排一个权值`val in [1, n]`，要考虑两个问题
这个权值安排给什么点？这个点要安排正数还是负数？

1）对于负数来说，如果`deg > 0`，它**只能向团中的点连边**
所以`负数点的 deg = 团的大小`

2）对于团呢？`团的 deg = 团的大小 + (绝对值小于 min{团的权值} 的所有负数点)`
考虑**动态扩张团和独立集**，并且**从绝对值大到小安排每个权值**，绝对值最大的几个负数已经被加入独立集中了
那么绝对值小于当前团权值 min 的所有负数点，也就是`n - |clique 的大小| - |独立集大小|`
`团的 deg = |clique 的大小| + 还未被考虑的点的个数`
（这也不难理解，因为从大到小安排权值，所以还未被考虑的点的绝对值，一定都会比当前的权值小）
（这也意味着，不管接下来这些点被安排到团中，或者安排到独立集中，它都会和当前点连边）

有了上述两点之后，就可以安排，哪些点是负数，哪些点是团了

按`deg`从小到大给每个点排序
1）先考虑`deg = 0`的点，绝对值最大的几个负数先安排给他们
2）然后迭代的每一步，考虑双指针，`l`考虑能不能进独立集，`r`考虑能不能进团
先考虑能不能扩张团，`deg`越大（对于右指针`r`），越有可能被加入团中，如果可以加入的话，先放一个进来
3）接着考虑`deg`较小的（左指针`l`），看看团的大小满不满足`deg`限制，如果不满足，就暂时不去动`l`
而是接着移动`r`去**扩张团**
否则就将左指针`l`加入独立集

## 2026牛客寒假算法基础集训营5
### H
**[智乃的矩阵](https://ac.nowcoder.com/acm/contest/120565/H)**
给定一个`n * n`的矩阵，现在有一个操作，每次选择`2 * 2`的连续子矩阵，选两对水平数字，或者两对垂直数字
让其中一对`+1`，另一对`-1`
问能不能把所有数都改成一样

**算法分析**
> 不难发现，每次操作，可能会修改局部的和，但是总和是不变的

所以如果能改成一样的数，最终改成的数是确定的，那就是`tar = sum / (n * n)`

> 考虑每次修改

```bash
case 1:
+1 +1
-1 -1

case 2:
+1 -1
+1 -1

compostion:
2 0
0 -2
```
一次修改，对角线位置$$(i, j), (i+1, j+1)$$，$$(i, j), (i+1, j-1)$$的奇偶性是保持不变的
不仅如此，**它们的和**也是会保持不变

根据这个观察，可以考虑**棋盘染色**
棋盘染色二分图模型，是指对于一个二维数组做二分图染色后，其颜色结构形如一个国际象棋的棋盘

对点进行分类，$$(i+j)$$奇数的一类，偶数的一类，考虑偶数的类有多少个点？假设有`c`个
因为**和`sumb`不变**，最终的数也不变，那么`sumb = c * tar`，如果不满足，就不行

> 再看看有什么特点？

```math
\begin{pmatrix}
+1 & +1 \\
-1 & -1
\end{pmatrix} \to
\begin{pmatrix}
0 & 0 \\
-2 & -2
\end{pmatrix} 
```
对于每一行/每一列，变化呈现如下形式
```bash
+2 0 +2 0 0 ..... +2 ...
或者是
+1 +1
	+1 +1
		+1 +1.....
```
局部可能奇偶性会有不同，**但是全局来看**，一整行的和，`diff = |修改前 - 修改后|`**必须是偶数**
对行/列依次检查即可

## Codeforces Round 1079
### C
**[C. Game with a Fraction](https://codeforces.com/contest/2197/problem/C)**
Alice and Bob 在博弈，给定两个数`p, q`，Alice 先手，除非`p = 0, q = 1`游戏停止，否则博弈一直进行
每次操作，令`p -= 1`或者是`q -= 1`

如果操作过程中，$$\dfrac{p}{q} = \dfrac{2}{3}$$，只要出现了这个数，`Bob win`，否则`Alice win`

**算法分析**
对于$$p \geqslant q$$，一定是`Alice win`，因为`Alice`先手，每一轮都令`q -= 1`
这样任何时刻都一定是$$p / q \geqslant 1$$

而对于$$\dfrac{p}{q} < \dfrac{2}{3}$$，这种情况也是`Alice win`
因为有不等式$$\dfrac{p-1}{q-1} < \dfrac{p}{q} < \dfrac{2}{3}$$，一旦比`2/3`小，就不会更大了

第三个结论是猜的，下面来证明，假设说$$p < q$$并且$$\dfrac{p}{q} \geqslant \dfrac{2}{3}$$，**Bob 总会获胜**
为什么，我们证明$$\dfrac{p - d}{q - d} = \dfrac{2}{3}$$，不难求出$$d = 3p - 2q$$
又因为$$\dfrac{p}{q} \geqslant \dfrac{2}{3} \Rightarrow 3p - 2q \geqslant 0$$

所以这样的$$\geqslant 0$$的`d`总是存在，这个`d`就是`Bob`后手跟进`Alice`的策略

## Codeforces Round 867 (Div. 3)
### G2. Magic Triples (Hard Version)
给定一个序列`a[1...n]`，求三元组的个数，三元组满足
```bash
1）1 <= i, j, k <= n
2） i, j, k 互不相同
3）存在一个正整数 b，使得存在 a[i], b*a[i], b*b*a[i]，即 (a[i], a[j], a[k]) 构成公比是 b 的等比数列
```
**算法分析**
对于$$a_i b^2 = a_k = O(10^9)$$，不难发现
如果$$a_i$$很大，那么$$b$$就很小，以$$a_i = O(10^3)$$分界，当$$a_i$$大于这个阈值的时候
那么$$b \leqslant O(10^3)$$，可以用`easy version`来枚举

如果$$a_i$$很小呢？那么$$b$$就很大，注意到此时$$a_i \leqslant O(10^3)$$
可以枚举原数组每个元素$$a_j$$，然后再枚举每一个可能的$$ai = 1 \sim O(10^3)$$
判断`ai`是不是原数组中的元素，只不过这里判断“是否出现”，用`bitset`，如果是直接`pos.contains()`好像会 TLE

## Codeforces Round 868 (Div. 2)
### D
**[CF1823D Unique Palindromes](https://codeforces.com/contest/1823/problem/D)**
用$$p(s, m)$$表示对于字符串`s[1...m]`（前缀`m`），有多少个不同的回文子串数
（注意，多个回文子串出现在不同位置，只算一次）
现在给定`n, k`，需要构造长度为`n`的字符串，`k`个条件分别是$$(x_i, c_i)$$
对于每个条件，构造出来的字符串**都必须满足**$$p(s, x_i) = c_i$$

**算法分析**
> 之前讨论过，如果一个串是回文串，那么一定存在一种划分，划分成两部分`L, R`，使得`L, R`**都不是回文串**

**[这个问题的讨论](https://www.ringalgo.com/article/80/)**

如果要构造一个串，使得它所包含的回文子串个数最小，那么一定是
```bash
abc abc abc ....
```
这样回文子串的个数是`3`（如果单个字符也算回文子串的话），那么最多呢？最多就形如
```bash
aaa....a
```

> 如果回文串多次出现只算一次，那么在回文串之后添加字符，会让前缀子串是回文的个数
**最多`+1`**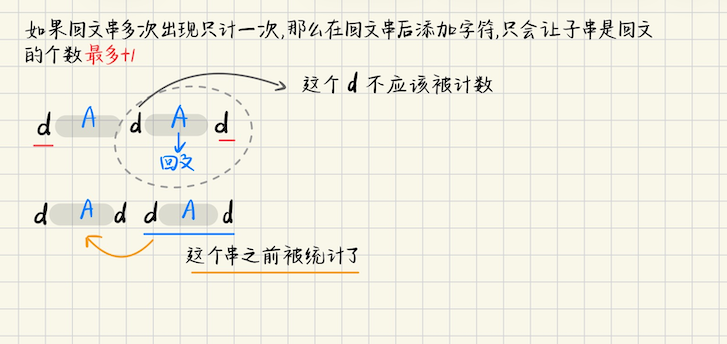
![](/media/content_img/cf868D.png)

所以很自然地，考虑增长情况，$$0 \leqslant \Delta c \leqslant \Delta x$$，如果不满足，直接输出`NO`

> 怎么去构造呢？考虑构造完全不增长

```bash
(a b c) (不在 {a, b, c} 中的其他字符) (a, b, c)
```
就可以构造完全不增长的情况

> 增长的情况呢？比如需要$$\Delta c$$

注意到`k`最多只有`20`，需要增长的时候，我们尝试引入一个新字符比如`e`
然后接上长度为$$\Delta c$$的`ee...e`即可
在后面接上`不增长模式，即 abc abc abc`

这样好像就可以做了，因为题目保证$$c_1 \geqslant 3$$
1）第一步，可以都统一先放一个`(a b c)`，然后看$$c_1$$还缺多少，放上`dd...d`，这样第一段就构造好了
2）从第二段开始，先满足$$\Delta c_i$$，添加一个新的字符，比如说是`e`，先放上$$\Delta c$$个`e`
然后呢？然后`abc abc`这样去接着放

> 坑点

为了不会冲突，避免产生`(a  ffff  a)`这样的情况，**不增长模式**，填充`abc`的时候，我们用一个**全局指针**
`idx = (idx + 1) % 3`，写一个`grow`函数，来实现字符串**用不增长模式填充到`dlen`**

### 回文串非常重要的性质

如果新加入一个字符`d`，之前有两个匹配的位置，`[d...d...] + d`，按下标排序$$d_1, d_2$$
那么$$S[d_2, d]$$是$$S[d_1, d]$$的**回文后缀**，也等于`Border`
也等价于$$S[d_2, d]$$是$$S[d_1, d]$$的**回文前缀**，换句话说，$$S[d_2, d]$$这个子串**一定已经出现过了**

上一篇：2026一月算法竞赛选题（三）下一篇：2026年二月算法竞赛选题（二）

看完文章有啥想法