2026一月算法竞赛选题（三）

[[ slider_text ]]

[[ item.c ]]

2026一月算法竞赛选题（三）

发布时间 2026-02-05 作者：秋千月 来源：算法小站

状态压缩dp 欧拉回路

## Codeforces Round 1077
### C
**[C. Restricted Sorting](https://codeforces.com/contest/2188/problem/C)**
给定序列`a`，找到最小的`K`，满足经过以下若干次交换，可以让`a`非严格单调递增
选择$$1 \leqslant i < j \leqslant j$$，其中要求$$|a_i - a_j| \geqslant K$$

**算法分析**
首先一定要有$$mx - mn \geqslant K$$，否则一定不能交换

二分一个`K`，那么$$mx, mn$$是可交换的
对于确定的$$a_i$$而言，$$\exists ?$$，满足$$|a_i - ?| \geqslant K$$

1）对于$$? - a_i \geqslant K \Rightarrow a_i \leqslant (? - K)$$，只要$$\exists$$一个值就可以了
于是$$a_i \leqslant \max(? - K)$$，只有$$a_i > mx - K$$时候才不满足
否则一定有$$a_i \leqslant (mx - K)$$，也就是说，$$a_i$$可以**和`mx`交换**

2）另外一种情况$$a_i - ? \geqslant K$$也是类似的，只要$$a_i \geqslant (mn - K)$$
就一定可以**和`mn`交换**

可交换的两个数，我们它们**在一个集合中**，于是我们就看看所有需要交换的位置是不是都在一个集合中即可
1）如果$$a_i, a_j$$是需要交换的，并且它们都可以和`mx`交换，那么用`mx`来作为**第三者**即可
```bash
mx, a[i], a[j]，接下来 a[i], a[j] 分别和 mx 交换
a[i], mx, a[j]
a[i], a[j], mx
mx, a[j], a[i]
```
2）对于`mn`的情况也是对称的

3）如果`a[i]`只能和$$mn$$交换，`a[j]`只能和$$mx$$交换呢？也是可以的，因为`mn, mx`是可交换的！
```bash
a[i] mn a[j] mx
mn a[i] mx a[j]

--> 交换 mx，mn
mx a[i] mn a[j]
a[j] a[i] mn mx
a[j] mn a[i] mx
```

### D
**[D. Shortest Statement Ever](https://codeforces.com/contest/2188/problem/D)**
给定两个数`x, y`，构造`p, q`，满足`p & q = 0`，并且$$|x-p| + |y - q|$$最小

**算法分析**
如果`x & y == 0`，那么直接让`p = x, q = y`，否则的话，需要对`x, y`**作出最小的调整**
选的`p, q`要尽量接近`x, y`

> 贪心策略

从高位开始考虑，一开始`p = x, q = y`，**高位尽可能保持不动**
什么情况下高位可以保持不动呢？`( (p & q) >> i & 1 ) = 0`，即`(p, q) = {(1, 0), (0, 1), (0, 0)}`
都是可以的，都可以不去动这一位

当`( (p & q) >> i & 1 ) = 1`的情况，**这一位是一定要动**，并且可能会损失$$2^i$$的代价

> 往大了改

为什么是可能？
因为这一位一定要改出一个`0`，如果往大了改，$$p > x$$，那么要改成最接近的，$$> x$$的数
同时这一位又必须是`0`，所以此时`p += (1LL << i)`，这样改成`....1 00...0`
从`i...0`这些位都是`0`

当然也可能不改，不改的话，那么这个`1`会由低位的进位来消除，这种情况我们枚举低位的时候会考虑到
当然如果通过低位的进位来消除，损失的代价可能是$$2^j$$，更小

所以枚举每一个`p, q 都是 1 的位 i`，采取这种策略，`p = ??..?1 00....0`，从`i -> 0`这些位都是`0`
那既然**低`i`位**都是`0`，对于`q`而言，这些位放什么数也都没什么所谓了
最优解当然是和`y`保持一致

前缀呢？分两种情况（我们把`p, q`都为`1`的位，称为`p, q`**冲突**）
1）从高位到第`i+1`位，之前都没有过冲突，那么自然`p, q`和`x, y`保持一致即可
高位一致，低位又不去改它，自然此时`q = y`是最优的

2）如果之前有过冲突怎么办？我们是希望改`i`位，通过`+(1LL << i)`进位的方式
消除更高位的冲突，但不希望去破坏更高位，因为进位引入的`1`有可能使得前缀`p & q != 0`破坏了更高的位
怎么办呢？此时我们不可能修改`2`个位，$$2^i + 2^j,  (j > i)$$的代价其实并不划算
因为我们可以构造`p = 011...1, q = 100...0`，此时修改`i`的代价$$\leqslant 2\cdot 2^i \leqslant 2^i + 2^j$$

3）如果第`i`位发生冲突，之后通过更低的位`j`的进位来消除`i, j`位的冲突，会怎么样？
如果这种情况发生，那么`[i...j] = 11..1`，这些位都是`1`，进位如多米诺骨牌一样
如果第`i`位的冲突，被第`j, (j < i)`位消除了，并且不会破坏更高的位，那再好不过了
如果破坏了更高的位，那么`p, q`第`i+1`位都是`1`，此时我们除了需要$$2^j$$代价来消除冲突之外
还需要额外$$2^{i+1}$$的代价来修复高位的“破坏”，而$$2^{i+1} = 2^i + 2^i$$
通过在`i`位操作`p = ....0 11...1, q = ....1 00...0`，损失的代价$$\leqslant 2 \cdot 2^i$$
**也是不劣的**

**综上所述**，这样的操作，**只会在一个位去引入`1`**，即`+ (1LL << i)`
通过进位的方式，一次性消除更高位的冲突，`q = y`保持一致

> 往小了改，$$p < x$$最大的数，并且在第`i`位是`0`
那么形如`p = (高位和 x 一致) 0 111..1`

如果`x, y`在第`i`位发生冲突，我们从高位到低位找到第一个冲突的位
```bash
p = ...(和 x 的高位保持一致) 1 .......
q = ...(和 y 的高位保持一致) 1 .......

可以这么修改
p = ...(和 x 的高位保持一致) 0 1 1 ... 1
q = ...(和 y 的高位保持一致) 1 0 0 ... 0
```
这样满足`(p & q) = 0`，并且损失$$\leqslant 2 \cdot 2^i$$，因为不涉及`+`的操作
所以高位并不会被破坏

另外，因为这个操作影响不到高位，所以不能指望通过低位的若干次操作合并来消除高位的冲突
只会一次性，改掉最高的，发生冲突的位，低位就都自动满足`p & q = 0`了

贪心地对$$p > x$$，`p`的第`i`位是`0`，并且`p 是 > x 的最小的满足条件的数`
以及$$p < x$$，`p`的第`i`位是`0`，并且`p 是 < x 的最小的满足条件的数`
对`ans`求一个`min`，对称地，对`q, y`的情况也做一遍即可

> 做法2，**数位 dp**

```bash
// sp = 0，当前 p 还未填
// sp = 1，当前 p 已经填的高位 < x，之后不管怎么填都会 < x
// sp = 2，当前 p 已经填的高位 > x，之后不管怎么填都会 > x
auto dfs = [&](auto &dfs, int i, int sp, int sq) -> i64 {
    if (i < 0) return 0;
    auto &res = dp[i][sp][sq];
    if (res < inf<i64>) return res;

i64 wgt = 1LL << i;
    int bx = x >> i & 1, by = y >> i & 1;

for (int mask = 0; mask <= 2; mask++) {
        auto bp = mask & 1, bq = mask >> 1 & 1;
        int nsp = sp, nsq = sq;

if (sp == 0) nsp = (bp > bx) ? 2 : (bp < bx ? 1 : 0);
        if (sq == 0) nsq = (bq > by) ? 2 : (bq < by ? 1 : 0);

i64 cost = 0;
        cost += 1LL * (nsp == 2 ? (bp - bx) : (bx - bp)) * wgt;
        cost += 1LL * (nsq == 2 ? (bq - by) : (by - bq)) * wgt;

i64 dpv = dfs(dfs, i-1, nsp, nsq);

if (chmin(res, dpv + cost)) {
            chose[i][sp][sq] = mask;
            to[i][sp][sq] = make_pair(nsp, nsq);
        }
    }

return res;
};

// 输出方案，(i, sp, sq) 表示当前状态
// chose(i, sp, sq) 表示当前这一位 p, q 应该分别填几
// to(i, sp, sq) = (nsp, nsq)，下一位转移到什么状态
dfs(dfs, LOG, 0, 0);
i64 ansp = 0, ansq = 0;

int sp = 0, sq = 0;
for (int i = LOG; i >= 0; i--) {
    auto mask = chose[i][sp][sq];

int bp = mask & 1,  bq = mask >> 1 & 1;
    if (bp) ansp |= (1LL << i);
    if (bq) ansq |= (1LL << i);

auto [nsp, nsq] = to[i][sp][sq];
    sp = nsp, sq = nsq;
}
```

## Educational Codeforces Round 163
### E
**[E. Clique Partition](https://codeforces.com/problemset/problem/1948/E)**
给定`n, K`，`n`个点的图，顶点编号$$1 \sim n$$，初始时候没有边
给每个顶点分配一个整数`a[i]`，所有的`a[i]`构成$$1\sim n$$的排列
之后对于$$(i, j)$$，如果满足他们的曼哈顿距离（关于点$$(i, a_i)$$），$$|i - j| + |a_i - a_j| \leqslant K$$
那么就在$$(i, j)$$连边，构造最大团（数量最小的团），每个顶点恰好属于一个团

**算法分析**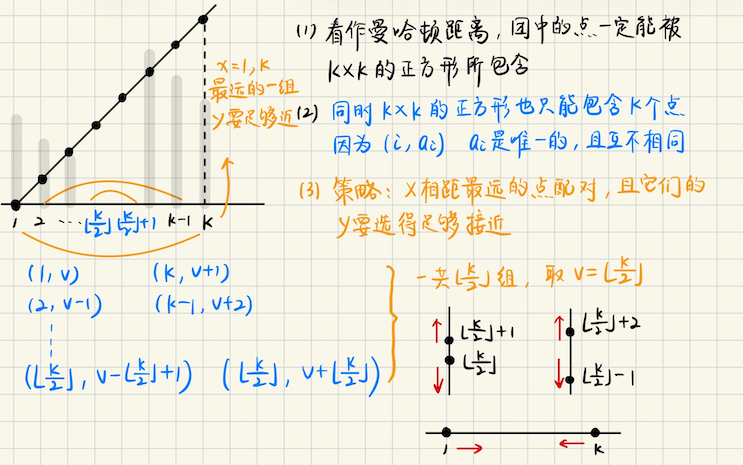
![](/media/content_img/EDU163E.png)

每$$k$$个分一个组，一共$$\lceil \dfrac{n}{k} \rceil$$个团
每一个组分别考虑，按上图所示的，`x`坐标两头配对构造

## European Championship 2024
### B
**[B. Charming Meals](https://codeforces.com/contest/1949/problem/B)**
给定两个序列`a`和`b`，长度都是`n`，两两配对，要使得$$|a_i - b_i|$$最小值最大
**算法分析**
这是一个**结论题**，最优配对一定是`a, b`排序后，将`a`的一段前缀和**相同长度的`b`的后缀**配对
枚举配对前缀的长度即可

相同长度的前缀，后缀匹配，又可以和**循环移位**相对应，枚举`b`的循环移位就可以

### I
**[I. Disks](https://codeforces.com/contest/1949/problem/I)**
平面内有`n`个圆盘，每个圆盘的半径都是正整数，没有两个圆盘有重叠，但是圆盘之间可能相切
确定是否能够改变圆盘的半径，使得
1）原来相切的仍然相切
2）没有两个圆盘有重叠
3）所有半径的和严格减小
4）不能改变圆盘的中心

输出 yes 或者 no

**算法分析**
每一组相切的圆构成连通分量，可以独立考虑，只要有一组能够满足“可减小半径”，答案就是`yes`
考虑一组连通分量，因为**不能改变圆盘的中心**，所以相切的两个圆，一个半径增加，另一个就要减小
并且$$(x_i - x_j)^2 + (y_i - y_j)^2 = (r_i + r_j)^2$$，$$(x, y)$$圆心是定值
因为要保持相切，$$r_i + \delta$$，那么就有$$r_j - \delta$$

只要是相切，要想继续保持相切关系，每一组连通分量$$\delta$$就是**确定的**
那就看有多少个圆是$$+\delta$$，多少个圆是$$-\delta$$

而相切的两个圆，必然是一个$$+\delta$$，一个$$-\delta$$，连边的话就构成了二分图
黑白二染色，如果`黑点的数量 != 白点的数量`，只要存在一个连通分量满足这个条件的话，答案就是`yes`

## Codeforces Round 937 (Div. 4)
### G
**[G. Shuffling Songs](https://codeforces.com/contest/1950/problem/G)**
给定一个`n`首歌组成的播放列表，每一首歌给出$$(g_i, w_i)$$，表示`(流派，作者)`
现在需要删除一些歌曲，使得剩下的歌曲，存在一种排列
使得相邻两首歌，要么有相同的作者，要么属于相同的流派（或两者兼有）
问需要最少移除多少歌曲？

**算法分析**
> 错误的做法

拆点，流派和作者看作独立的点，那么对于歌曲$$i$$，$$(i, g_i), (i, w_i)$$连边
然后看一下这个图是否连通
这样做是不对的，因为**图连通不等于图中存在所有点组成的哈密顿路径（单链路径）**
**反例如下**
```bash
A (Pop,1)
      |
    B (Pop,2) —— D (Rock,2) —— C (Rock,3)
      |            (作者都是2，互相连通)
    F (Jazz,2)
      |
    E (Jazz,4)
    
    (注：G 也在中间，和 B,D,F 连在一起，因为作者都是2)
```

> 尝试从哈密顿路径角度来考虑

哈密顿路径只能考虑**状态压缩**，记$$dp(mask, i)$$表示当前已经选的数的状态是`mask`
并且**以`i`结尾**（当然`i`必须是`mask`中为`1`的位）
枚举要加入哪个歌曲`j`（当然`j`必须是为`0`的位），有转移
```bash
if 歌曲 i 和歌曲 j 能匹配上
	dp(mask | (1 << j),  j) <--- dp(mask, i) + 1
```

## 2026牛客寒假算法基础集训营1
### H
**[Blackboard](https://ac.nowcoder.com/acm/contest/120561/H)**
给定长度为$$n$$的序列`a[1...n]`，其中由若干个`+`连接，即`a[1] + a[2] + ... + a[n]`
现在把一些`+`改成`|`，并且规定`|`的运算优先级更高，问有多少种改法
使得改了之后的结果和改之前相同
两种方案是不同的，当且仅当存在至少一个位置，使得在原来方案中，这个位置是`+`
而在新的方案中，这个位置是`|`

**算法分析**
根据`a + b = (a | b) + (a & b)`
假设说对于位置$$i$$，如果$$i$$之前存在一个位置$$j$$，使得`a[i....j]`的位，**两两都是`0, 1`错开**
那么这部分的`(a & b)`就可以“擦去”，我们称可以将这些位置和$$i$$**合并**

很显然，对于特定的$$i$$，需要找到最左边的满足条件的`l`
这可以用双指针，维护一个全局的`cnt[0...31]`表示这每一位有`几个 1`，如果`max(cnt) > 1`
那么不合法，`l++`

这样我们可以知道$$j \in [l, i]$$，这些位置都可以和$$i$$合并
那么$$last = j - 1$$，存在转移
```math
\displaystyle
dp(i) = \sum_{last \in [l-1, i-1]} dp(last)
```
计算`dp`值的时候，维护前缀和`sum`，`dp[i] = sum[i-1] - sum[l-2]`
然后`sum[i] = sum[i-1] + dp[i]`
```bash
dp[0] = 1, pre[0] = 1;
int l = 1;

vector<int> cnt(LOG+5, 0);

auto add = [&](i64 x) -> void {
    for (int j = 0; j < LOG; j++) {
        if (x >> j & 1) cnt[j] += 1;
    }
};

auto del = [&](i64 x) -> void {
    for (int j = 0; j < LOG; j++) {
        if (x >> j & 1) cnt[j] -= 1;
    }
};

for (int i = 1; i <= n; i++) {
    add(a[i]);
    while (*max_element(cnt.begin(), cnt.end()) > 1) {
        del(a[l]), l++;
    }

auto dpv = pre[i-1] - (l >= 2 ? pre[l-2] : 0);
    dp[i] = dpv;

pre[i] = pre[i-1] + dp[i];
}

cout << dp[n] << "\n";
```
## European Championship 2024
### F
**[F. Dating](https://codeforces.com/contest/1949/problem/F)**
软件有`n`个用户，编号是`1-n`，每个用户有一个偏好的活动列表，活动编号是`1-m`
如果两个用户都喜欢的活动个数$$\geqslant 1$$，并且两个用户都各自有至少一个自己喜欢而对方不喜欢的活动
那么这两个用户是匹配的，找到可能的匹配，或者报告不存在

**算法分析**
什么情况下认为是匹配，考虑**活动被覆盖了多少次**
如果存在$$\geqslant 1$$个活动被覆盖了`2`次，并且存在两个活动，被染成不同的颜色，那么这样陪配对就合法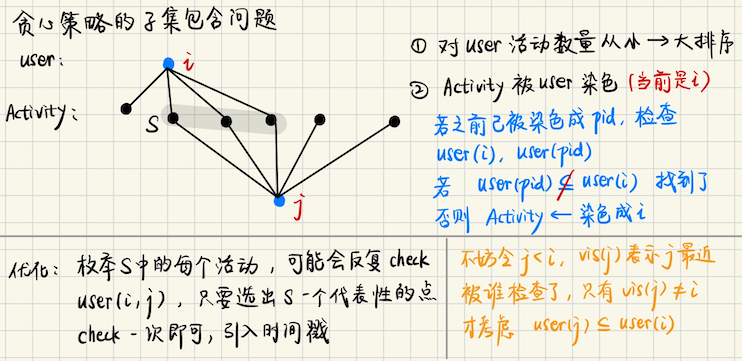
![](/media/content_img/EC2024F.png)

只不过判断$$user_j \subseteq user_i$$的时候，不要用`std::include`，而是`for x in sma`
**二分查找**`big`中是否含有`x`

### G
**[G. Scooter](https://mirror.codeforces.com/contest/1949/problem/G)**
校园内有`n`栋建筑，编号从`1-n`。每栋建筑安排一堂数学课或一堂计算机课，或者没有安排任何课程（不能同时安排两门课）
此外，每栋建筑最多有一位教授，这位教授要么擅长数学，要么擅长计算机科学
选择车辆从任意顺序访问建筑，**每栋建筑只能访问一次**，要求行程结束后，
每栋安排了数学课的建筑必须有一位数学教授，每栋安排了计算机课的建筑必须有一位计算机教授
设计一条路线，使得所有课程都可以进行

车辆每次只能接受一名教授移动，并且不能将教授刚送走又接上
drive 每次只能去往不同的建筑

#### 简化版问题
**[简化版问题 C - Alternated](https://atcoder.jp/contests/abc421/tasks/abc421_c)**
给你一个长度为 2N 的字符串 S，S 中恰好包含了 N 个 A 和 N 个 B
求使 S 中没有相邻的相同字符所需的最少操作次数(可能为零)，一个操作能交换 S 中相邻的两个字符

目标序列是确定的，要么是`ABAB...`，要么是`BABA...`
也就是说，`A`要么都在奇数位，要么都在偶数位，而一旦确定了`A`，`B`也就随之确定了

那么这样的问题，原序列`A`能去往的最优位置（交换代价最少）是确定的，比如目标序列`ABAB...`
第`1`个`A`去往`1`
第`2`个`A`去往`3`
第`3`个`A`去往`5`
以此类推，这样就能算出最优代价了

#### 供给-需求模型
假设说没有`-`会怎么样，发现如果`s[i] != t[i]`，是**无解的**
比如说要交换`C,M`，`到建筑 1 接送 C ---> 送到建筑 2，接下 M ---> 返回建筑物 1 送 M`
而这是无法完成的，因为题目规定一个建筑物只能访问一次（但路径可以折返交叉）
也就是说，**交换环，如果没有供应（入边）的话，是无解的**

所以可以对节点进行分类
```bash
供给点：
-M, -C

交换点：
CM, MC

需求点：
M-, C-
```
针对这三类点，那么很显然应该从供给点取“教授”，**贪心地**，根据刚才的分析，如果所有供给点消失的话
交换点`(C, M), (M, C)`是无法被满足的

比如说从供给点`-C`取出`C`，接着应该**优先去往**交换点`CM`，如果所有交换点都被满足的话，才去到纯需求点`C-`
对于`M`也是类似的策略

#### 欧拉回路
但是这样做会`WA on testcases 34, invalid Pickup`，为什么？
因为这个问题中可能有**多余的供应**，比如说
```bash
demand:		-  C
supply:		  C M
```
最终的`(C, M)`的这一组 M 会被扔掉，晾在一旁不管它（不需要把教授接回家）

> **一个点只能访问一次，想到了什么？欧拉回路！点的位置看成边的`id`，跑欧拉路径！**

![](/media/content_img/EC2024G.png)

将多余出来的形如`(C, M)`的边，将其供应端换成起点`-`（因为欧拉回路必须`indeg = outdeg`）
输出方案，建反图跑**欧拉回路**即可，可以用 Hierholzer 算法来输出方案

上一篇：2026一月算法竞赛选题（二）下一篇：2026年二月算法竞赛选题（一）

看完文章有啥想法