2026一月算法竞赛选题（二）

[[ slider_text ]]

[[ item.c ]]

2026一月算法竞赛选题（二）

发布时间 2026-01-24 作者：秋千月 来源：算法小站

数论分块 括号序列

## Codeforces Round 1073 (Div. 2)
### D1. Sub-RBS (Easy Version)
**[D1. Sub-RBS (Easy Version)](https://codeforces.com/contest/2191/problem/D1)**
我们认为一个括号序列`a 比 b 更好`，当且仅当以下两个条件之一成立
1）`b`是`a`的前缀，即`a`比`b`更长（越长越好），但是$$a \neq b$$
2）如果存在第一个字符不同的位置，`a[i] = (`但是`b[i] = )`

现在给定一个合法的括号序列，记为`s`，长度是`n`
对所有非空的，`s`的子序列（不要求连续）`t`，使得`t`是合法的括号序列，并且要求`t`的长度尽可能长
问最长的长度是多少？

**算法分析**
括号序列**重要的性质**
1）**非负性**，任意位置前缀和非负
2）**平衡性**，`(`的数量和`)`的数量相等，即`s[n] = 0`（`s`表示前缀和）

#### 贪心性质

那么所有合法的括号序列，**把`(`全部都放在前面，`)`全部都放在后面，一定是最优的**
因为前缀和要非负，贪心地，越大越好，`(`尽可能放在前面
另外这样的操作不会改变平衡性

所有的合法括号序列，都可以看作`( ( ( ... ) ) )`（即全部`(`在前，全部`)`在后的序列），`)`往前**经过若干次交换**形成

### D2. Sub-RBS (Hard Version)
**[D2. Sub-RBS (Hard Version)](https://codeforces.com/contest/2191/problem/D2)**
括号序列**“更好”**的定义和 D1 一样，对于任意括号序列`t`，定义它的分数
1）如果`t`不是合法括号序列 RBS，分数是`0`
2）如果存在一个合法括号序列`r`，**比`t`更好**，那么得分是**最长的，更好的， RBS（必须合法）** 的长度`|r|`
3）不存在更好的，得分是`0`

现在给你一个字符串`s`，求它的所有非空子串（不需要连续）的得分之和，对`998244353`取模

**算法分析，几个重要的性质**
#### 合法括号序列的性质
给定一个合法的括号序列 RBS，任意删除一个`)`，并且在这个位置之后，如果还能再任意删除一个`(`的话
删除这两个字符构成的括号序列，仍然是合法括号序列

> 证明并不难，首先任意位置删除`)`，不仅不会破坏“前缀和非负”，反而会使得前缀和`+1`
之后再找位置删除`(`，又恰好使得前缀和`-1`，和之前的`+1`**抵消了**
删一个`(`再删一个`)`，也是不会改变平衡性的

#### 推论一
删掉形如`) (`模式的字符（两个字符不要求连续，$$0 \leqslant i < j < n$$，`s[i] = ( 且 s[j] = )`即可）
之后可以在任意位置，交换一下变成`( )`模式再插入，仍然是一个合法括号序列
也就是说，删除`) (`，会使得合法括号序列**不唯一**，因为你不知道删的是`) (`还是`( )`

> 证明也不难，根据之前的分析，删掉`) (`，剩下的仍然是一个合法括号序列
那么加入`( )`，首先不会违反平衡性，另外，在任意位置加入`(`，只会使得前缀和增大`+1`
而之后加入`)`，又使得前缀和`-1`**相抵消**

**合法括号序列**删除`) (`（不要求两个字符连续），总是可以做到的
删除`( )`却是有条件的

#### 推论二
在合法括号序列中删除`( )`是有条件的，如果能够**成功**找到一个位置能删掉`(`
在这个位置之后删掉`)`是没有限制的

1）在前缀和恰为`0`的前缀`[1...i]`中，`(`是不能被删掉的，找不到可删去的`(`
也就意味着`)`也删不掉

2）如果前缀和`[1...i]`恰好`= 1`，在其中删掉一个`(`，`i`之后再任意删掉一个`)`，括号序列是唯一的

> 因为你删掉`(`，那么意味着前缀和`s = 0`，那么还原回来，能不能补上`)`？显然是不能的
否则前缀和就变成`-1`了，不合法，所以删掉的一定是`(`而不可能是`)`

3）如果前缀和`[1...i]`$$> 1$$，在其中删掉一个`(`，`i`之后再任意删掉一个`)`，括号序列不唯一

> 因为即使删除一个`(`，仍会使得前缀和$$\geqslant 1$$，可以容纳一个`)`，被删掉的括号
可能是`(`也可能是`)`

#### 算法设计
这个问题只要根据推论一就可以做出来，假设说`t`是一个 **RBS**
什么时候，存在一个合法的子序列`r`，`r`是 **RBS** 并且`r`更优呢？

1）一定是`t`存在某个位置是`)`，不要了，用之后的`(`来代替这个位置
2）这样就相当于**你删除一个**`)`，你既然删除一个`)`，就必须要再删除一个`(`
而后面你拿出一个`(`来代替`)`，还必须有一个`(`**可供删除**

当且仅当存在模式`)(... (`时，存在一个最小子串`r`，`|r| = |t| - 2`并且`r`更优，得分是`r`

> 首先可以跳过`)`，直接用下一个位置的`(`来代替它，这样操作相当于在原来的基础上删掉一个`)`
根据推论一，这总是可以做到且不违法的
接着在`(`之后，如果还能找到一个位置是`(`，那么也把它删掉，这样就保持了合法括号序列的**平衡性**

根据`D1`的**贪心性质**，给定一个合法括号序列，只要能够在`)`后面找到一个`(`
说明一定存在一个`)(`结构，其中`)(`**相邻**
（因为合法括号序列可以看作`( ( ( ... ) ) )`若干个`)`往前交换）

那么只要判断，如果能在`)( ... (`，`)(`结构后面再找到一个`(`，就表示存在合法括号子序列`r`
贡献是`|t| - 2`
（因为`)...(`可以删掉，剩下的序列仍然是 RBS）

这样可以用**记忆化 dp + dfs**来做，`dfs`考虑`s`当前字符选或者不选
```bash
dp(i, bal, sgn, len) 表示当前考虑 s[i]，[0...i-1] 的前缀和是 bal
sgn 表示当前处于 ") ( (" 的那种状态，len 表示当前选择的字符串的长度

1）递归出口，如果 i >= n，当且仅当 bal = 0 and sgn = 3 才有得分 len - 2
2）其他情况，记忆化，考虑 s[i] 选或者不选
```
```bash
unordered_map<arr, mint, hashfun, eqfun> dp;

auto dfs = [&](auto &dfs, int i, int bal, int k, int len) -> mint {
	if (dp.contains(arr{i, bal, k, len})) return dp[arr{i, bal, k, len}];
	mint &res = dp[arr{i, bal, k, len}];

if (i >= n) {
		if (bal == 0 and k == 3) return res = max(len - 2, 0);
		return res = 0;
	}
	// 不选当前字符
	res += dfs(dfs, i+1, bal, k, len);
	// 选当前字符，考虑处在什么状态
	if (str[i] == '(') {
		auto nk = k;
		if (k >= 1) nk = min(3, nk + 1);

auto nbal = bal + 1;
		auto dpv = dfs(dfs, i+1, nbal, nk, len + 1);
		res += dpv;
	}
	else {
		auto nk = k;
		if (k == 0) nk += 1;
		auto nbal = bal - 1;
		if (nbal >= 0) {
			// 剪枝
			auto dpv = dfs(dfs, i+1, nbal, nk, len + 1);
			res += dpv;
		}
	}
	return res;
};
```

## 括号序列扩展问题
### 牛客暑期多校训练营4 G
**[Ghost in the Parentheses](https://ac.nowcoder.com/acm/contest/108301/G)**
**问题描述**
有一个有效括号序列，但是，每个字符有$$1/2$$的机会被替换成`?`，问得到的序列，能够构造出**唯一**括号序列的方案数

**算法分析**
首先，所有的`)`可以替换成`?`，不影响结果，方案数是$$2^{n / 2}$$

接着考虑一部分`(`和一部分`)`替换成`?`
根据推论`1`，形如`) ... (`要是替换的话，会导致括号序列不唯一
所以要替换成`?`，**只能是选一段后缀，把`)`替换成`?`，把前缀`(`替换成`?`**

那就简单了，枚举`)`的位置`i`，钦定后缀`[i+1...n]`的`)`都要改成`?`，而`[1...i]`前缀中的`)`不去动
计算贡献，贡献取决于`[1...i]`中能改多少个`( --> ?`

这个很好求，后缀的贡献就是$$2^{suf(i+1)}$$
而前缀呢？根据性质`2`，前缀能改出多少个`?`，取决于`[1...i]`中**最后一个前缀和等于`1`的位置`j`**
这个也是很好预处理的，用`le(i)`表示

前缀能贡献的方案数是$$2^{le(i)}$$
综上所述，方案数就是$$2^{le(i)} \cdot 2^{suf(i+1)}$$

## Codeforces Round 939 (Div. 2)
### D
**[D. Nene and the Mex Operator](https://codeforces.com/contest/1956/problem/D)**
给定一个长度为`n`$$(\leqslant 18)$$的序列`a`，用不超过$$5 \cdot 10^5$$次操作，每次操作如下
选取$$l, r$$，并且求`mex(a[l], a[l+1], ....., a[r])`，然后把`a[l...r]`都改成`mex`
现在要最大化`a`数组的和（不必最小化操作次数），并且输出一种操作方案

**算法分析**
如果不输出方案，怎么做？因为$$n \leqslant 18$$，所以`mex`最多就是`18`
如果`a[i]`本身就足够大，那么不动`a[i]`
这样就可以设计一个状态压缩，二进制枚举**那些位置不动**，这样不动的位置就把序列分割成若干连续的段
每一段$$[l, r]$$依次考虑可以操作变成多少？

> 操作序列怎么维护？

**性质**
给定长度为`m`的**全`0`序列**`[0, 0, ....., 0]`，通过取区间`mex`操作，能够把区间所有数都变成`m`

操作的过程是**递归的**，考虑$$m = 3$$对应的`[0, 0, 0]`
1）递归地，很容易知道`[0, 0] --> [0, 1]`能够改成`[0...len-1]`的排列
2）考虑`[0, 0, 0]`，先递归处理后面的`[0, 0]`，`[0, [0, 1]]`
再对整段区间取一个`mex`，这样就改出了整段`[2, 2, 2]`
3）最后一个`2`不要动它，前面的`[2, 2]`**回退到**`[0, 0]`，又可以重新改成`[0, 1]`
综上所述可改成`[0, 1, 2]`

```bash
solve(l, r) 表示将区间 [l, r] 改成关于 {0...len-1} 的排列，所得到的操作序列，其中 [l, r] 一开始全 0
	solve(l+1, r)
	
	ops.emplace_back(l, r)，这样整个区间值都是 {r-l}
	将 i in [l...r-1] 全部回退成 0，操作序列是 ops.emplace_back(i, i)
	
	solve(l, r-1)
```
### C
**[C. Nene's Magical Matrix](https://codeforces.com/contest/1956/problem/C)**
给定一个$$n \times n$$的矩阵`a`，一开始都是`0`，两种操作
```bash
op 1:	选择任意一行，将这一行填充成 1-n 的排列
op 2:	选择任意一列，将这一列填充成 1-n 的排列
```
最大化$$\sum a\_{i, j}$$

**算法分析**
手模后发现，最优矩阵形如
```bash
1 2 3 4
2 2 3 4
3 3 3 4
4 4 4 4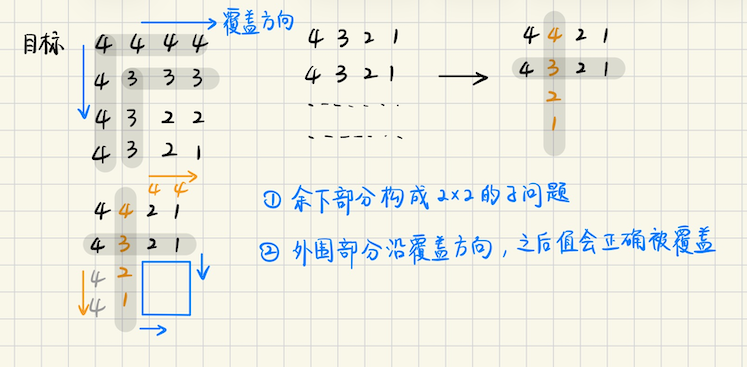
```
![](/media/content_img/cf939c1.png)

## Educational Codeforces Round 164
### E
**[Chain Reaction](https://codeforces.com/contest/1954/problem/E)**
有`n`个怪物排成一排，第`i`个怪物有`a[i]`点生命值，**每一秒**可以选择一个存活的怪物
对其释放一次连锁闪电，闪电对怪物造成`k`点伤害，并且向左向右传播（传播耗时忽略不计）
对每个存活的怪物也造成`k`点伤害，到达队列开头结尾，或者遇到怪物死亡，则停止传播
问消灭所有怪物所需要的最小秒数，对$$k \in 1\sim \max(a[1\cdots n])$$输出答案

```bash
[5, 2, 7]，k = 3
如果从第三个怪物开始打，打到 2 把第二个怪物打死
闪电还是会继续传播，直到下一次操作（下一秒），2 这个位置才会被阻隔
```

**算法分析**
> 看一个结论题

**[E. Hard Design](https://www.ringalgo.com/article/78/)**
给定一个正整数序列，选定$$[l, r]$$，使得$$[l, r]$$中的所有数都`-1`，最少要几次操作
答案是确定的，$$\sum \max(0, a\_{i} - a\_{i-1})$$

那么这个问题，答案也是类似，对于$$k$$，最少需要操作的次数是
```math
\displaystyle
f(k) = \sum_{i = 1}^{n} \max(0, \lceil \dfrac{a_i}{k} \rceil - \lceil \dfrac{a_{i-1}}{k} \rceil)
```
**整除分块**可以做
![](/media/content_img/edu164E.png)

## Codeforces Round 938
### E
**[E. Long Inversions](https://codeforces.com/contest/1955/problem/E)**
给定一个长度为`n`的`01 串 s`，任选一个`k`，做若干次如下操作，反转字符串中连续`k`个字符
目标是使得`s`变成`全 1 串`，输出满足条件的最大的`k`

**算法分析**
算法实现起来并不难，注意到`1`位置要被覆盖偶数次，而`0`位置要被覆盖奇数次
不难发现，如果是第一个位置是`1`，那么它是不能被覆盖的

所以从前往后贪心是对的，每一次反转考虑第一个出现`0`的位置，反转`[p, p+k-1]`这一段就可以了

比较难的是算法实现，好在**区间异或**，可以一边维护差分数组，一边维护前缀和
```bash
记 cur 表示当前位置的前缀和
diff 表示差分数组

for i = 0 to n-1:
	cur ^= a[i]，cur 此时维护了差分数组的前缀和
	
	bit = a[i] ^ cur，是 a[i] 反转后实际的值
	if (bit == 0):
		需要反转，[i, i+k-1]，如果 i+k-1 >= n，是不能够反转的，return false
		否则就可以反转
		
		cur ^= 1, diff[i+k] ^= 1;

return true
```
暴力`check`每一个`k`即可

### F
**[F. Unfair Game](https://codeforces.com/contest/1955/problem/F)**
给定一个序列，只有`{1, 2, 3, 4}`这`4`个数，总共有`n`个数，现在你是裁判
每一轮只要所有的数`xor 和 = 0`，那么`Bob`得分，否则不得分
每一轮结束，Eve 会任意拿走一个数
这样游戏会执行`n`轮，假设 Eve 用最优策略，目标是最大化 Bob 得分，输出这个最大得分

**算法分析**
首先，`Bob`得分的**充要条件是**
1）`4`的个数`cnt[4] mod 2 = 0`必须为偶数
2）`1, 2, 3`的个数，要么都是奇数，要么都是偶数

那么根据这样的条件，很容易写出`dp(cnt1, cnt2, cnt3, cnt4)`的记忆化`dp`，但是会超时

**一种优化方法**
由于每次修改，我们只关心`cnt{1, 2, 3, 4}`**个数的奇偶性**，设计状态的时候，只考虑当前这个数有奇数个还是偶数个

那么问题来了，如果`cnt = 0`，继续取它是非法的，怎么办呢？
实际上可以**倒着做**，一开始所有数都是`0`，每一次任选一个数令 cnt `+1`
最后考虑状态`r[i] = cnt[i] mod 2,    dp(r0, r1, r2, r3)`即可

这样做还会有一个问题，那就是，如果一个数比如是`4`，**加过头了怎么办？**
此时我们只需要检查奇偶性，只要奇偶性和`dp(r0, r1, r2, r3)`**最终状态奇偶一致**
说明加过头，那一定是被加了**偶数次**这个数

而一个数被加了偶数次，**`xor 和`是不变的**
只要保证这个`dp`的过程进行了`n`次就可以

即使算过头了，因为对答案有贡献的永远是`xor 和 = 0`的状态
对一个数的`cnt`加减偶数次不影响答案

只要是$$(r0, r1, r2, r3)$$（其中$$r_i = cnt_i \bmod 2$$），保持一致的状态
这些状态**都被视为是同一种**状态，**至于`cnt`的值具体是多少，不需要关心**
（只要在这些状态内部，那么就可以相互转化，不需要额外代价）

> 另外，`for i = 0 to n-1`，只能做`n-1`次迭代，因为第一次`(0, 0, 0, 0)`虽然也是合法状态
但是不得分，因为一开始什么数都没有

**一种贪心方法**
容易看出，`cnt4`一定要偶数，所以`4`对答案的贡献一定是$$\lfloor \dfrac{cnt4}{2} \rfloor$$
那么考虑`cnt1, cnt2, cnt3`，如果他们都是奇数，选择是将他们都拿走`1`

如果是偶数呢？那么肯定优先选择$$\lfloor \dfrac{cnt}{2} \rfloor$$，每`2`次操作换一次贡献
而要想贡献奇数的话，那必须**每`3`次操作**才能换一次贡献，所以只有它们一开始都为奇数的时候贡献一次
剩下情况，都是在偶数下操作

## Codeforces Round 1075 (Div. 2)
### C1 C2
**[C2. XOR-convenience (Hard Version)](https://codeforces.com/contest/2189/problem/C2)**
构造一个排列，使得对任意下标$$1 \leqslant i \leqslant n-1$$，都**存在一个**$$i \leqslant j \leqslant n$$
满足$$p_i = p_j \oplus i$$，或者报告不存在

**算法分析**
首先`p[n]`可以随便放，不妨考虑简单的情况，就$$p_n = 1$$
那么如果**奇偶配对**的话，**相邻两个奇偶**，总可以凑成`2k ^ 1 = 2k+1, (2k+1) ^ 1 = 2k`
那么就有形式 $$(i, i \oplus 1), (i \oplus 1, i)$$

如果$$(i, p_i)$$连边的话，就会形成**若干大小为`2`的环**，环上的元素恰好为相邻两个`(偶，奇)`组合
这样 C1 就做完了

> C2 怎么做

首先，如果`n`是奇数的话，`a[n] = 1`，那么`n - 1`一定是偶数
偶数总是可以分解成若干大小为`2`的环，环上的元素是相邻的奇偶，这一定可以做到

那如果`n`是偶数呢？偶数会出现**恰有一个无法配对**的情况

如果$$n = 2^k$$（是`2`的幂），我们猜可能是不合法的，否则的话，这个值放在哪里呢？
这个值$$\oplus$$任何一个下标$$idx \in [1, n]$$，要么是$$\oplus n = 0$$，要么是$$\oplus$$之后$$> n$$
不论如何也构不成排列

否则的话，我们是可以构造的
把`1`放在`p[n] = 1`，这样`n - 1`就是奇数了
```bash
i:			n-2		n-1(奇数)
p[i]:		n-1		n-2(偶数)

形如
i:				(xx..x10)		(xx..x11)
p[i]:			(xx..x11)		(xx..x10)
```
这样下去，只有`n`无法配对，并且留在`p[1]`处，**而这是不合法的**
因为`n`是偶数，$$n \oplus 1 > n$$，构不成排列！

> 那么`n`放在哪里呢？很自然地想到，可以考虑 n ^ (下标) = n ^ (lowbit(n))

可以令`下标 = lowbit(n)`，即`n`最低位的`1，比如说 1000`，`swap(a[1], a[lowbit(n)])`，这样可以吗
```bash
i:			1000
p[i]:		xx..x(1000)

考虑 i = lowbit(n) 这个位置，(i ^ p[i]) = 1000(更高位会有1)...(0000)
这个值必然比 p[i] 大，根据我们的构造方法，必然可以在 i 之后找到
```
那么此时`a[1]`应该是多少呢？原先`lowbit(n) = 1000`，这个位置放的是`1001`
```bash
i:		1
p[i]:	1001

那么很显然 (i ^ p[i]) = 1000，1000 在之后能不能找得到呢？
注意到原先，下面这一组
i:		1001
p[i]:	1000
我们并没有动它！1000 在 (i, p[i]) = (1001, 1000) 的组合中！
```
这样我们就构造完了

上一篇：2026.1月算法竞赛选题（一）下一篇：2026一月算法竞赛选题（三）

看完文章有啥想法