算法小站
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
登录
注册
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
十二月算法竞赛选题(一)
概率与期望,01trie,周期,border,Z函数,前缀函 .....
[[ slider_text ]]
[[ item.c ]]
0
0
十二月算法竞赛选题(一)
发布时间
2025-12-11
作者:
秋千月
来源:
算法小站
差分
字符串
Z函数
## Codeforces Round 956 ### E **[E. I Love Balls](https://codeforces.com/problemset/problem/1983/E)** Alice 和 Bob 在玩球,有`n`个球,其中有`k`个特殊球,每个球有权值 Alice 先手,一个回合随机选一个球,并且将权值加到自己的得分上,初始得分都是`0` 被选中的球会被删除,如果能选中特殊球,并且游戏中还剩至少一个球,那么该玩家继续 否则轮到对方操作,问 Alice 和 Bob 的期望得分 **算法分析** > 不难发现,两个人的期望得分,一定是所有球的权值之和,现在只考虑 Alice 先假设说没有特殊球 这个怎么算呢?考虑**每个球是否对 Alice 有贡献** 注意到,对于当前的球,只有把它放在奇数位上,它才会对 Alice 有贡献,球和球之间是独立的 并且概率都是相等的,一共有$$n - k$$个特殊球,有$$\lceil \dfrac{n-k}{2} \rceil$$ 个奇数位置 所以对于每个球,都是**等概率的**,$$p = \lceil \dfrac{n-k}{2} \rceil / (n - k)$$ 那么答案就是$$\sum p \cdot a_i = p (\sum a_i)$$ > 那么特殊球呢? 考虑特殊球什么时候有贡献,用**插板法**,考虑将特殊球插入普通球的空位中 Alice 拿到特殊球,**意味着他一定能拿到紧随其后的普通球**,也就是说 能被 Alice 拿到的特殊球,一定在**能被 Alice 拿到(奇数位置)的普通球**前面的空位中 一共有$$(n - k + 1)$$个空位(包括最后一个空位,特殊球后面不接任何普通球也是可以的) 能被 Alice 拿到的**空位编号**,也必须是**奇数** 每个特殊球仍然是等概的,$$p_s = \lceil \dfrac{n-k+1}{2} \rceil / (n - k + 1)$$ 答案是$$p_s \cdot sum_s$$,其中$$sum_s$$表示特殊球的权值之和 ## 2025 ICPC 武汉 ### H **[H. Restore the Array](https://qoj.ac/contest/2609/problem/14726?v=1)** 交互题,给你一个长度为`n`的序列,数是两两不同的,但是不知道每个数具体的值是多少 可以询问最多`2n - 2`次,每次询问`? c`,`c`你自己选 交互器会返回一个值`res`,值是$$\max(a_i \oplus c)$$,要你还原数组`a` **算法分析** 之前用**位分治**来解决过这个问题 但是给定一个数`c`,查询已有集合中,$$\oplus c$$最大的数,有经典做法,就是`01-trie` > 用 01 字典树来解决这个问题 首先`ask(0)`可以得到`max`,再`ask(max)`又可以得到一个数 将它们插入字典树,不难发现 **具有公共前缀 + 分岔点** > 考虑最高位分叉点(从高位往低位第一个分岔点),一边往`0`走,一边往`1`走 假设说我们还原出了数$$x,y$$,分叉点所在的位是$$p$$,$$x_p = 0, y_p = 1$$ 现在就考虑$$x$$,**注意到** ```bash 1) 从最高位到 p 位 ask: [111...1] [00...0] xor x = ( [topbit....p 位] 和 x 的高 p 位一样的数 ) ask(x ^ ( ~0U << p )) 这样一定能问出一个前缀 [top...p] 和 x 一样的数 2) 接下来就看后缀,[p+1...0] 位,假设存在一个数和 x 的前缀一样,但不知道,记为 ? 就取低位后缀看 [00...0] xor x = (x 的后缀) [00...0] xor ? = 问出来的数 = (单单看后缀几位的最大值) ``` 换句话说,每一个分叉点,我们都可以问出**前缀和 x 相同,后缀**就看**截断**`[p+1...0]`这几位能够得到的最大值 当然问出的最大值可能和$$x$$相同,那也就意味着再往下都不会有分叉点了 否则问出的数一定$$\neq x$$,并且$$> x$$,构成前缀和$$x$$相同的数的**上界** 随着分叉点的下移,这个上界不断减小,直到$$x$$ 问出来一个数就插入 01-trie 中,对$$y$$也是如此 > 具体看算法实现 从高位往低位找分叉点,比如第$$bit$$位是$$c$$,trie 树指针用`p`表示 如果`tr(p, c) = nullptr`,就动态开点,同时若发现`tr(p, !c) != nullptr`,说明`bit`就是分叉发生的位 这时候,对于$$x$$,要查询`x xor (~0U << bit)` 对于$$y$$,要查询`y xor (~0U << bit)` 为了方便获取`x, y`具体值到底是多少,每一次动态开点的时候,就标记一下这个点对应的具体值是多少 后续每插入一个新的数,都会导致分叉点下移 > 因为我们已经把最大的数找出来了,而我们再一次`ask(max)`,那么$$(\oplus \max)$$最大的数 必然是**和`max 0-1`分叉在最高位的数** 沿着某个分支下去,我们再询问的数,依然是前缀和`x`都一样,**后缀截断`[00...0]`**这`bit`位中 和`x 截断低 bit 位`**分叉相对也在最高位的数** 这样做下去,就导致分叉点一定从高位到低位不断下移的 可以用一个队列来存下需要`ask`的数,每`ask(x)`,就`insert(x ^ ask)` 在`trie`和答案数组中同步插入 `trie`中每插入一个新的数,就寻找新的分叉点,并且询问新的`x, y`对应的分叉位 往下还有没有数没有找到,把对应的`ask`的数再放入队列中,直至队列为空 #### 算法实现 **Trie 树部分** ```bash namespace Trie { const int N = 1e5 + 5; const int MASK = (1U << 30) - 1; int LOG = 30; int trie[N * 32][2]; // 需要维护的,树中的分叉点,具体对应的值 // 以及当前可能会新加入的,需要询问的一些数 cand i64 val[N * 32]; queue<int> cand; void insert(i64 x, int t = 1) { int p = root; sz[p] += t; for (int i = LOG; i >= 0; i--) { int u = x >> i & 1; if (!trie[p][u]) { trie[p][u] = newNode(); val[ trie[p][u] ] = x; if (trie[p][!u]) { int x = val[ trie[p][u] ], y = val[ trie[p][!u] ]; int askx = (MASK & (x ^ (~0U << i))); int asky = (MASK & (y ^ (~0U << i))); cand.push(askx), cand.push(asky); } } p = trie[p][u]; sz[p] += t; } } }; ``` **solution 部分** ```bash void solve(int cas) { int n; cin >> n; using namespace Trie; set<int> res; auto mx = ask(0); insert(mx), res.insert(mx); cand.push(mx); while (cand.size() && res.size() < n) { auto x = cand.front(); cand.pop(); auto xmax = ask(x); // debug(getmx(x)); auto exist = xmax ^ x; insert(exist), res.insert(exist); } out(res); } ``` **Trie 树技巧** 分叉点会变化的时候,需要动态开点 在动态开点的时候,可以打标记,标记这个点对应的原来的值是多少 方便做后续的处理 ## Codeforces Global Round 26 ### D **[D. "a" String Problem](https://codeforces.com/contest/1984/problem/D)** 给定一个由小写字符组成的字符串$$s$$,请问有多少个非空字符串`t != "a"`,使得可以将$$s$$分成若干子串 满足,每个子串要么是`t`要么是`"a"`,至少要有一个子串等于`t` 划分的意思是$$s = t_1 + t_2 + \cdots + t_k$$ **算法分析** > 咋一看好像和周期有关 和周期有关的问题,想到两个方面,`border`以及`Z 函数` 1)`周期 + border = n`(这里周期和 border 都是指长度) 2) Z 函数 2.1 字符串下标假设说从`0`开始,`[0...i-1]`构成一个最小整周期 那么有$$i + Z(i) = n$$ 2.2 本质不同的子串,可以增量构造,`S`每次加入一个字符`c` 令`t = reverse(S + c)`,对`t`求前缀函数 那么加入这个字符`c`,对本质不同子串的贡献是` += |t| - Zmax` 其中`Zmax`表示`t 中所有位置 i`,对应的$$\max Z(i)$$ > 这里用前缀函数(Z 函数)来求解,满足条件的划分应该是什么样的? 找到所有非`a`的字符,处理出它们第一次出现的位置,用`l, r`分别表示位置的最小值,最大值 那么$$t$$至少应该是`s[l, r]`这么长,当然可能会更长 划分模式是`(若干 a) + t + (若干 a) + t + .... + t + (若干 a)` 假设说最小的划分单位是$$t$$,考虑可能有如下符合的情况 1) `t`后面不接`a`,只会在`t`前面接上若干`a` 2) `t`后面接上若干`a`,同时也会在`t`前面接上若干`a` **情形一** 如果`t`后面不接`a`,只可能在`t`前面接上若干`a`,构成一个合法的新的`t` 注意到`t + (若干 a) + t`,预处理出从某个下标`i`开始,最多有连续的几个`a` 那么`t`前面最多能接多少个`a`呢?假设说是`can`个 对于特定的`t`,考虑`t`与`t`之间间隔的`a` `can = min(间隔的 a 的个数,包括 S 中最开始的前缀 a)`,那么对答案的贡献是`can + 1` `+1`是因为可以不加任何`a`,如果要加`a`就可以在前面加`[1...can]`个 **情形二** 如果是`t`后面接着`a`呢?形如`[a...a] + t + [a...a]`,实际上 令`t = t + [a...a]`作为新的`t`,枚举`t`的长度这很容易,在新的`t`中考虑,前面最多能加几个`a` > 把模式算出来之后,就考虑判断合不合法 什么时候合法呢?注意$$S$$要处理一下,去除前导`a`,求出前缀函数 枚举$$t$$(实际上是一个前缀),从小到大枚举前缀,考虑每一个$$t$$的段(中间有连续的`a`就跳过) 开始的位置假设是$$j$$,当且仅当对每一个段的开始,$$Z(j) = |t|$$时,合法 > 技巧,怎么算从一个位置开始,有多少个连续的`a`,用`ext(i)`表示`i`能往前延伸的最大长度 从后往前`for` ```bash for i = n downto 1 ext[i] = (str[i] == 'a' ? ext[i+1] + 1 : 0) ``` ### E **[E. Shuffle](https://codeforces.com/contest/1984/problem/E)** 给定一个`n`个节点的树`T`,对整棵树进行恰好一次的洗牌操作,利用原来的树节点 构造一棵新的树$$T_2$$,有`3`个步骤 1.从原树中任意选择一个节点$$V$$,以$$V$$为根,创建一棵新树$$T_2$$ 2.将$$V$$从`T`中移除,原树形成若干个子树 3.对每个子树都重复如上操作,并且洗牌后的子树的根节点,再连回$$V$$中,完成新树的构建 (注意,子树的这样操作是不断进行的,叶子结点是度数为 1 的点,如果根节点只有一个儿子,那么根节点也是叶子结点) 问能获得的最大叶子结点数是多少? **算法分析** 将操作**分成若干层**,每一次操作,对应每一层取出一个根,然后在**下一层**递归处理剩下的子树 > 初步观察,能够发现 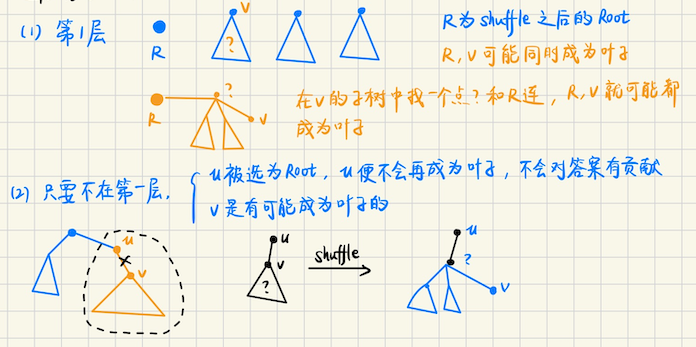 > 考虑几种特殊情况,以及递归求解 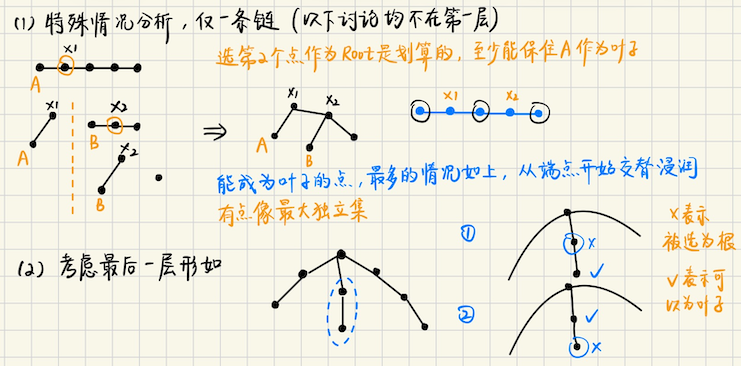 > 发现类似最大独立集问题 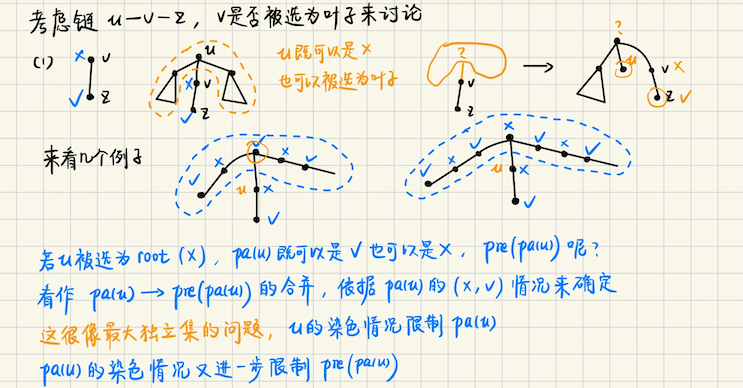 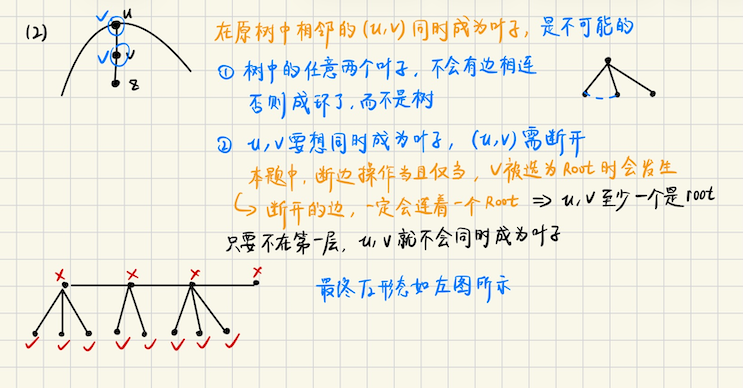 不难发现,符合条件的叶子树,是一个**强化版的最大独立集**,满足 1)最多只允许有一个点和它的父亲同时被选,作为第一层的`root`和`子树的叶子` 2)除此之外,任意一条边上的两个点,**不能同时被选为叶子** 在这种情况下的树的独立集大小 那这个怎么做呢?因为只会有一个点和它的父亲,即$$(u, pa_u)$$可能同时被选为叶子 那么我们可以枚举这个点,树上的枚举,考虑**换根 dp** 我们先正常跑一遍树的最大独立集,得到`dp 数组` 换根 dp 考虑三个东西,`u 往上 (不包括 u) 的补集的最大独立集 up(u)`,`u 及其子树的最大独立集 dp(u)` 以及枚举$$(u, v)$$时候,`rem = (u 及其子树扣除 v 这个分支之后,还剩下的部分)` 根据这三部分去转移 特别注意,对于$$x$$,`up(fa) + rem1 + dp(x, 0)`此时算的是`x`不被选为叶子(也就是说被选为子树的根)的最优解 如果`deg(x) == 1`,还要`+1`,因为题目中要求`deg = 1`的根节点也要计算进去 `res = ( up(fa) + rem1 + dp(x, 0) ) + [deg(x) == 1]`,`chmax(ans, res)`即可 #### 算法实现 ```bash up(x, 0/1) 表示 x 往根方向的补集(不包括 x),父亲 fa 会不会被选(注意是父亲,而不是自己) dfs(x, fa),考虑 fa 被选的状态,维护 x 子树的补集 1)要在 dp(fa) 对应的状态中,扣除 x 相关分支的信息 2)考虑根据 fa 是否被选,维护补集大小 rest0, rest1 auto rest0 = rem0 + max(up(fa, 0), up(fa, 1)) auto rest1 = rem1 + up(fa, 0) chmax(ans, dp(x, 0) + (g[x].size() == 1) + max(rest0, rest1) ) chmax(ans, dp(x, 1) + rest0) ``` 具体实现换根的第二遍 dfs 如下 ```bash void solve { auto dfs2 = [&](auto &dfs2, int x, int fa) -> void { // 扣除 x 这个分支对应的状态 auto rem0 = dp[fa][0] - max(dp[x][0], dp[x][1]); auto rem1 = dp[fa][1] - dp[x][0]; // fa status 0/1 auto rest0 = rem0 + max(up[fa][0], up[fa][1]); auto rest1 = rem1 + up[fa][0]; chmax(ans, dp[x][0] + max(rest0, rest1) + (g[x].size() == 1)); chmax(ans, dp[x][1] + rest0); up[x][0] = max(up[fa][0], up[fa][1]) + rem0; up[x][1] = up[fa][0] + rem1; for (auto y : g[x]) { if (y == fa) continue; dfs2(dfs2, y, x); } }; for (auto x : g[1]) { dfs2(dfs2, x, 1); } } ``` ## Codeforces Round 952 ### H2 **[H2. Maximize the Largest Component (Hard Version)](https://codeforces.com/problemset/problem/1985/H2)** 给定一个$$n \times m$$的网格,每个网格中的数,是`.` or `#`,上下左右`4`个方向,相邻的格子是可达的 对于`#`单元格,如果能够移动到其他`#`单元格,称它们是连通的,所有可达的`#`就构成一个连通分量 现在一次操作,可以选择任意行或者任意列,然后将选取的行或者列,每个单元格都设置成`#` 问`#`所有连通分量中,最大的是多少 困难版,是要求同时选择$$(r, c)$$,将$$r$$行和$$c$$列同时都改成`#` **算法分析** > 简单版怎么做? 简单版并不难做,先对所有连通的`#`用并查集处理一下 然后枚举修改的列(行也是对称地,再做一次) 1)`add = 修改的列 . 的个数` 2)操作完成之后(假设操作的是`y`列),`y-1 and y+1`所有的`#`连通快都会彼此连通(通过`y`) 只要用`set`记录一下`y-1 and y+1`列`#`所在的连通快的编号(即所在的并查集的根) 答案就是`sum(所有相邻列的连通块的 size) + add`,用这个值来更新`ans`即可 > 困难版呢?在于说我们`for`$$(r, c)$$,是$$O(nm)$$复杂度,再对每一个$$(r, c)$$进行统计`add` 又有一个$$O(n + m)$$的复杂度,总的复杂度时$$O(n^2m + m^2 n)$$,可能无法接受 但一开始枚举$$O(nm)$$是可行的,但需要在$$O(1)$$或者$$O(\log )$$内计算出答案 那能不能通过预处理,比如说,把$$r$$两侧的连通块先预处理到`set(r)`中 同样也预处理`set(c)`中,在计算的时候,直接取`set(r)`和`set(c)`的并 这样做在极端情况下,是要耗费$$O(n)$$的时间的,复杂度又变成了$$O(n^m)$$ 如果先求和呢,`sumset(r), sumset(c)`,也是不行的,因为这样我们只知道他们两侧的连通快的大小之和 并不知道这些连通快的具体编号,可能某一个连通快,同时位于`r and c`的一侧 它的`size`被加了`2 次`,这样会重复计算,也不行 > 但这个好像启发我们,可以一个连通块一个连通块地考虑 一个极大的连通块,考虑最上方和最下方,最左端和最右端,构成了$$(xl, xr, yl, yr)$$的矩形区域 矩形的左上角是$$(xl, yl)$$,右下角是$$(xr, yr)$$,假设当前连通块是$$C$$ 单独考虑行和列的话,如果你要对$$x \in [xl-1, xr+1]$$的行来操作,那么这样的行对应的答案 都要算上这个连通块$$C$$ 换句话说,连通块对$$x \in [xl-1, xr+1]$$有贡献,这些行的答案都要$$+|C|$$ 对于$$y \in [xl-1, xr+1]$$也是如此 但这样会有重复,因为这个问题要求同时对$$(x, y)$$操作,也就是说,对于连通块$$C$$ 你选$$x \in [xl-1, xr+1]$$,但是你$$y \notin [yl-1, yr+1]$$,把$$y$$选在外面,那是不会重复的 而如果你选的$$(x, y)$$,刚好落在$$(xl-1, xr+1, yl-1, yr+1)$$围成的矩形区域内 那么这个$$C$$会被多算一次 > 最后要解决的问题是,对于每一个连通块$$|C|$$,可以很方便求出$$(xl-1, xr+1, yl-1, yr+1)$$ 但是怎么让矩形区域中的点都$$+|C|$$呢? 首先,之前的操作让$$(xl-1, xr+1)$$和$$(yl-1, yr+1)$$都加上$$|C|$$,这个操作很简单 **差分数组**单点修改即可,最后求具体的某个$$x$$的时候,就是求差分数组在$$x$$的前缀和即可 现在呢?怎么让一个矩形区域都$$+|C|$$,可以用二维前缀和 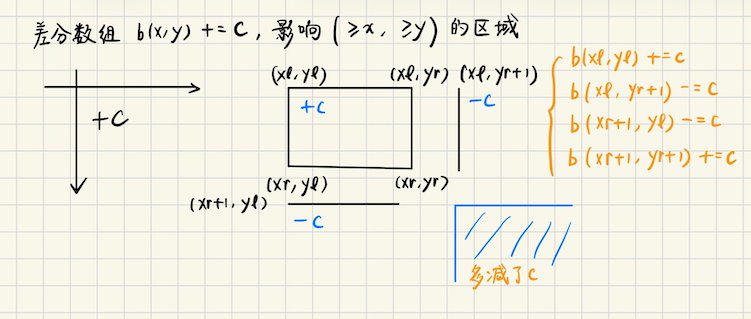 ## Codeforces Round 954 (Div. 3) ### G1 **[G1. Permutation Problem (Simple Version)](https://codeforces.com/contest/1986/problem/G1)** 给定一个排列$$p$$,长度是$$n$$,问有多少对下标$$(i, j), 1 \leqslant i < j \leqslant n$$ 满足$$(i \cdot j) \mid (p_i \cdot p_j)$$ **算法分析** 不难发现,可以先$$/ gcd(p_i, i)$$,即$$\dfrac{a_i}{b_i} \dfrac{a_j}{b_j}$$ 此时有$$(a_i, b_i) = 1, (a_j, b_j) = 1$$,那么所求的下标,满足限制 ```math \displaystyle \begin{cases} b_j \mid a_i \\ b_i \mid a_j \\ i < j \end{cases} ``` 不妨令$$(a_i, b_i)$$表示$$\dfrac{a_i}{b_i}$$ ```bash 对于特定的 i,找 j > i,并且 (a[i], b[i]) <--> (a[j] 是 b[i] 的倍数, b[j] 是 a[i] 的因子) ``` 这样的统计可以**开一个桶**来解决,一般是**遍历一个限制的桶**,然后查询另一个限制 ```bash 倒着 for i = (a[i], b[i]) (1) 考虑先满足 > i 的 j,b[j] | a[i] 的限制 for a[i] 的因子 bj,在 bj 的桶 buc[bj] 中,我们希望能够知道 有多少个 aj 满足 aj 是 b[i] 的倍数 这就需要维护 buc[bj][x] = 有多少个形如 {x, 2x, ..., kx} 的数? 这样的话,就可以让 ans += buc[ bj ][ b[i] ] (2) 考虑维护,当前的 a[i] 对 (b[下标 < i 的数] | a[i]) 有贡献 for a[i] 的所有因子 d, buc[ b[i] ][d] += 1 ```
0
0
上一篇:算法竞赛选题——概率与期望(四)
下一篇:十二月算法竞赛选题(二)
看完文章有啥想法
发布评论
249 人参与,0 条评论