算法竞赛选题——概率与期望（四）

[[ slider_text ]]

[[ item.c ]]

算法竞赛选题——概率与期望（四）

发布时间 2025-12-07 作者：秋千月 来源：算法小站

概率和期望 矩阵

## Educational Codeforces Round 121
### F
**[F. A Random Code Problem](https://codeforces.com/contest/1626/problem/F)**
给定一个数组`a`以及整数$$k$$，执行下面的代码
```bash
long long ans = 0;
for (int i = 1; i <= k; i++) {
	int idx = rnd.next(0, n - 1)
	// 生成 [0, n-1] 区间的随机数，包括端点 0, n-1, 每个数被选中的概率相同
	
	ans += a[idx]
	a[idx] -= (a[idx] % i)
}
```
计算此代码执行后，ans 的期望

**算法分析**
从值域来考虑，枚举每个**可能出现的数**$$x$$，枚举每个位置**对答案的贡献**
假设说是求出的`ans`，答案就是
```math
\displaystyle
\mathbb{E}(ans) = \sum_{\text{ans is possible}} ans \cdot \dfrac{1}{n^K}
```
那么问题要求$$\mathbb{E} \cdot n^{K}$$，实际上就是对所有合法的`ans`，求$$\sum ans$$

> 考虑每个位置对答案的贡献

对于$$i = 1\to k$$，假设这个位置填的是$$a_i$$，那么它对答案的贡献是`a[i] * (除了 i 之外的其他位置填数的方案数)`
注意到$$[1, i-1]$$每个位置有$$n$$种选择，$$[i+1, K]$$每个位置也有$$n$$种选择
所以对每个$$i$$，贡献是$$a_i \cdot n^{i-1} \cdot n^{K-i}$$

> 另外，$$a_i$$不是确定的，而是随机的，要考虑$$a_i$$可选的值的范围
```bash
idx = 随机一个 [0, n-1]
ans += a[idx]
```
也就意味着，$$a_i$$可能的取值，会取遍$$a[0\cdots n - 1]$$中所有的数

综上所述
```math
\displaystyle
\sum ans = \sum_{i = 1}^{K} \left( \sum_{j = 0}^{n-1} a_j \cdot n^{i-1} \cdot n^{K-i} \right)
```

> 计算$$\sum a_j$$，可以从值域上考虑，考虑可能出现的每个数，以及它可能出现的次数

考虑一个数$$x$$出现的次数，可以用**动态规划**来求解，根据每一次迭代，选或者不选$$x$$
定义$$dp(i, x)$$表示第$$i$$次迭代，$$x$$一共出现了多少次，有转移

1.不选$$x$$，$$\displaystyle dp(i+1, x) \leftarrow dp(i, x) \cdot \binom{n-1}{1}$$

2.选$$x$$，注意我们枚举的是上一个阶段可能的$$x$$，$$dp(i+1, x - x \bmod i) \leftarrow dp(i, x)$$

这样做的复杂度是$$O(nk)$$，在$$n = 10^{7}$$肯定不行

> 优化

注意到$$(x - x \bmod i)$$一定会变成`i 的倍数`，$$x$$要变，要么变成$$x$$的倍数
如果$$x$$本来就是$$i$$的倍数，那么$$x$$是不会变的

也就是说，$$x$$要变，就一定会变成$$i = [1, 2, \cdots, k-1]$$的倍数，也就是它们的`LCM`
这个值是`LCM = 720720`

那好了，如果$$a_i < lcm$$，可以暴力，按照之前的`dp`式子去转移
暴力求出每个位置$$i \in [1, K]$$，每个数$$x$$对答案的贡献，即`dp(i, x)`

当然这里求出来的是$$[1\cdots i]$$中，$$x$$对答案的贡献，$$[i+1, K]$$可以随便放，没有限制
后半部分对答案的贡献是$$n^{K - i}$$，$$x$$对答案的贡献就是$$dp(i, x) \cdot n^{K - i}$$

至于$$a_i \geqslant lcm$$的情况呢？可以预先处理
1.如果变，就一定会变到`a[i] - a[i] % lcm`，记为$$a_i'$$**（是`lcm`的倍数）**，那么$$i$$位置可以有的候选值是
```math
\displaystyle
a_{i1}' \cdot n^{k-1}, a_{i2}' \cdot n^{k-1}, a_{i3}' \cdot n^{k-1} \cdots
```
对于$$i$$位置，可以贡献的答案是，所有可能的`a[i] - a[i] % lcm`加起来，值是`sum`，$$sum \cdot n^{K-1}$$
而$$K$$个位置，每个位置皆是如此，$$K \cdot sum \cdot n^{K-1}$$就是答案

2.考虑不变，如果$$a_i$$本身就是`lcm`的倍数，那么$$a_i$$是不会变的，这部分答案在上面已经讨论过了
那就是考虑$$a_i \bmod lcm \not \equiv 0$$的情况
注意到表达式，`a[i] * (其他位置的方案数) = ( (a[i] - a[i] mod lcm) + (a[i] mod lcm) ) * (其他位置的方案数)`
可以将`mod lcm`的部分和`lcm 的倍数的部分`拆开来分开计算
而`lcm`的倍数的部分，是不会变化的（不管你变还是不变），这部分在`case 1`的分析中已经预处理了
所以只需要考虑`mod lcm`的部分，这部分的值的计算，按照`dp`方程来算即可
因为`lcm = 720720`，可以在$$O(7 * 10^5)$$内做完，假设余数是$$x$$，贡献是$$x \cdot dp(i, x) \cdot n^{K - i}$$

> 算法核心

算法的思路在于，`lcm`的倍数和`mod lcm`部分分开来计算，方案数单独统计，然后相加

## 牛牛写作文
**[牛牛写作文](https://ac.nowcoder.com/acm/contest/32282/H)**
现在有$$n$$个句子，随机选一些构成一篇文章，等概率进行操作
1.停笔，结束作文
2.写下第`1`个句子
3.写下第`2`个句子
4.`.....`
5.写下第`n`个句子

每个事件发生的概率都是$$\dfrac{1}{n+1}$$
现在给定一个字符串`s`，问`s`出现在文章中的概率，$$n \leqslant 1000, |S| \leqslant 200$$

**算法分析**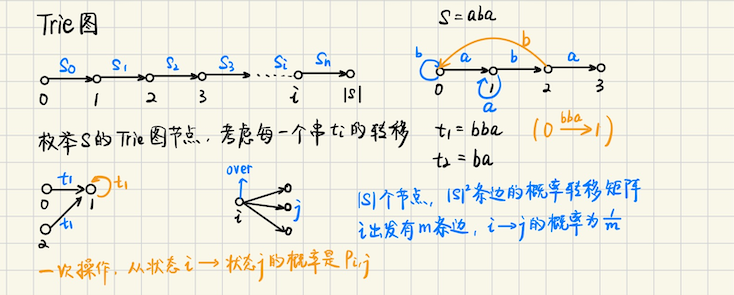
![](/media/content_img/nowcoder32282H.png)

> 一次操作，有$$p = \dfrac{1}{n+1}$$的概率直接结束，同时有$$1 - p = \dfrac{n}{n+1}$$的概率从`Trie图`的一个状态转移到另一个
最终我们要考虑的是，若干次操作之后，$$p(0, |S|)$$的值是多少

不难发现，一次操作从$$i \to j$$的概率，就是`Trie图转移概率矩阵`$$P(i, j)$$的值
两次操作呢？从$$i\to j$$的概率是多少？需要枚举中间转移到哪个点，所以是
```math
\displaystyle
\sum_{k = 0}^{|S|} P_{i, k} \cdot P_{k, j}
```
实际上就是**矩阵乘法**，$$\bold{P}^2(i, j)$$，那么如果操作了$$k$$次（写`k`个句子）
从$$i \to j$$的概率就是$$\bold{P}^k(i, j)$$

> 那么这种概率问题，是一种类似几何概型，假设说$$k$$次结束

一次就结束，那么概率很显然是$$\dfrac{1}{n+1} \cdot \bold{I}$$
如果是$$k$$次呢？那么需要有$$k-1$$次用来写句子（即`k-1`次的矩阵概率转移），然后最后一次用来`over`
所以概率是$$\displaystyle \left(\dfrac{n}{n+1} \right)^k \bold{P}^{k} \cdot \dfrac{1}{n+1}$$
```math
\displaystyle
\bold{M} = \lim_{k \to +\infty} \dfrac{1}{n+1} \bold{I} + \dfrac{1}{n+1} \dfrac{n}{n+1} \bold{P} + \cdots + \dfrac{1}{n+1} \left(\dfrac{n}{n+1} \right)^k \bold{P}^k + \cdots \\
=\dfrac{1}{n+1} \left(\bold{I} - \dfrac{n}{n+1}\bold{P} \right)^{-1}
```
最后一项表示矩阵的逆

> 补充，`trie图`构建，参考`AC 自动机`

如果`nxt(i, ch) = 0`，说明`i`这个节点**没有**`ch`的后继边，**需要跳 border 链**
此时`nxt(i, ch) = nxt( fail(i), ch )`，另外，`fail`值呢？**既然都失配了**，`[.... i] + ch`这个后缀肯定和前缀不一样
`([...i] 的 border) + ch`才有可能成为新的`border`，此时沿着`border 链`去找就可以了，`fail( nxt(i, ch) )`不需要更新
因为`fail( nxt(i, ch) )`是跳回到`([....i] 的 border) + ch`去找`border`，而`([....i] 的 border) 的 border`
即`fail`值已经求出来了，可以直接继承到`i`这个节点，`fail`不需要更新

如果`nxt(i, ch) != 0, is not empty`，说明`i`这个节点已经有了`ch`的后继边了，`nxt(i)`无需动它
但同时也意味着，`i 的 border`也可以接上`ch`，换句话说，**在`i`处出现了一段相同的前缀和后缀**
就意味着要更新`border 链了`，如下图所示
![](/media/content_img/nowcoder32282H-02.png)

### 算法实现
**特别注意**
在状态$$|S|$$这个点，一定要构造**吸收态**，此时不管怎么转移，都是成功找到想要的句子
也就是说，`mat(|S|, |S|) = 1`

```bash
void solve(int cas) {
    int m;
    cin >> m;

vector<string> T;
    for (int i = 0; i < m; i++) {
        string ti;
        cin >> ti;
        T.emplace_back(ti);
    }

string str;
    cin >> str;
    int n = str.size();

vector nxt(n+1, vector<int>(26+5, 0));
    for (int i = 0; i < n; i++) {
        int ch = str[i] - 'a';
        nxt[i][ch] = i + 1;
    }

vector<int> fail(n+1, 0);
    for (int i = 1; i < n; i++) {
        for (int ch = 0; ch < 26; ch++) {
            if (nxt[i][ch] == 0) nxt[i][ch] = nxt[ fail[i] ][ch];
            else fail[ nxt[i][ch] ] = nxt[fail[i]][ch];
        }
    }
    // debug(fail);
    Matrix<mint> mat(n+1, n+1);

for (int i = 0; i < n; i++) {
        for (auto ti : T) {
            int cur = i;
            for (auto c : ti) {
                cur = nxt[cur][c - 'a'];
                if (cur == n) break;
            }
            mat.data[i][cur] += mint(1) / mint(m);
        }
    }
    mat.data[n][n] = mint(1);
    auto I = mat.E(n+1);
    I -= mat * (mint(m) / mint(m+1));

auto inv = I.inv();
    inv *= mint(1) / mint(m+1);

auto ans = inv.data[0][n];

cout << ans << "\n";
}
```

## 一些常用的期望模型
**恰好 i 次成功**
假设成功的概率是$$p$$，那么实验进行恰好$$i$$次的概率是$$(1 - p)^{i-1} \cdot p$$
也就是说，实验成功的**期望**是
```math
\displaystyle
\sum_{i = 0}^{\infty} i \cdot (1-p)^{i-1} p = p\cdot \sum_{i=0}^{\infty} i(1-p)^{i-1}
```
其中求和部分相当于**几何级数的求导**，即$$\dfrac{1}{(1-x)^2} = \dfrac{1}{(1-(1-p))^2} = \dfrac{1}{p^2}$$
综上所述，期望恰好是$$\dfrac{1}{p}$$

## Min-Max 容斥
**[Ex - Random Painting](https://atcoder.jp/contests/abc242/tasks/abc242_h)**
有$$n$$个编号从$$1 \sim n$$的格子，一开始都是白色的，同时给定$$m$$个球
重复以下操作，直到所有的$$n$$个格子都变成黑色
1.从箱子中随机取一个球
2.设取出的球是$$x$$，将格子$$[l_x \cdots r_x]$$全部涂黑
3.放回取的球

问将所有格子涂黑所需要的操作次数期望值

**算法分析**
**求操作到某个状态才停止的期望操作次数**，有一种方法叫做** min-max 容斥**
这个问题求什么？假设所有的格子集合是$$S$$，记$$\max(S)$$表示`S 中最晚被染色的格子，它被染色的时间`
同理，$$\min(S)$$表示$$S$$中的所有格子，第一次被染色的时间
```math
\displaystyle
ans = E(\max(S)) = \sum_{T \subseteq S} (-1)^{|T|+1} E(\min(T))
```

那么假设说我们有一个子集（即部分格子）$$T$$，考虑$$E(\min(T))$$怎么求呢？
假设说有$$c$$条线段能够命中（即覆盖到）$$T$$中的元素，那么$$p = \dfrac{c}{m}$$
经过$$i$$次操作，命中的概率就是$$(1-p)^{i-1} p$$，这是一个几何概型

根据上面的分析，$$E(\min(T))$$就是$$T$$中元素被命中的期望，恰好是$$\dfrac{1}{p} = \dfrac{m}{c}$$

于是我们就转而求
```math
\displaystyle
\sum_{T \subseteq S} (-1)^{|T|+1} \cdot \dfrac{m}{c}
```

> 考虑$$c$$怎么求，以及$$|T|$$怎么算

只需要关心$$c$$，以及$$|T|$$中的元素的奇偶性，很自然地想到`dp`，考虑$$i = 1 \to n$$，每个格子选或者不选
可以枚举$$|T|, c$$，其中$$|T|$$只关心其奇偶性，这样表达式可以写成
```bash
(c, |T|) 状态的方案数 * (m / c)
```
这里方案数用`dp`来求
记$$dp(i, c, |T|)$$表示考虑$$i$$这个位置**强制**加入$$T$$，此时命中$$i$$这个格子的线段有$$c$$个
而$$T$$中元素个数的奇偶性恰好是$$|T|$$的方案数

转移的话，需要枚举上一个加入$$T$$中的元素是$$k \in [1, i-1]$$，上一个状态比如说是$$dp(k, c, |T|)$$
那么怎么转移呢？

那么新加进来的点是$$i$$，需要知道，左端点在$$[k+1\cdots i]$$，并且右端点$$\geqslant i$$的线段有`cnt`个
而这可以暴力预处理完成

> 枚举每个线段$$[l, r]$$，枚举它有贡献的区间，右端点可以允许的位置是$$j = [l \to r]$$
左端点呢？左端点可以允许的位置是$$i = [1 \to l]$$，这些位置`tot[i, j] += 1`
这个线段，对左端点在$$[i\cdots j]$$处，右端点$$\geqslant j$$的线段个数，有`1`的贡献

令`cnt = tot[k+1, i]`，就存在转移
```math
\displaystyle
dp(k, c, |T|) \xrightarrow{k\in [1, i), \quad +=} dp(i, c+cnt, |T| \oplus 1)
```

> 统计答案

枚举最后被加入$$T$$的元素$$i$$，枚举$$c = 1 \to m$$，枚举$$|T| \in \\{0, 1\\}$$
计算`ans += (-1 or 1) * dp(i, c, |T|) * (m / c)`

### 算法实现
```bash
void solve(int cas) {
    int n, m;
    cin >> n >> m;

using pint = pair<int, int>;
    vector<pint> seg(m+1);

for (int i = 1; i <= m; i++) {
        auto &[li, ri] = seg[i];
        cin >> li >> ri;
    }

// debug(seg);
    vector cnt(n+5, vector<int>(n+5, 0));
    for (int i = 1; i <= m; i++) {
        auto [li, ri] = seg[i];

for (int x = 1; x <= li; x++) {
            for (int y = li; y <= ri; y++) cnt[x][y] += 1;
        }
    }

vector dp(n+5, vector(m+5, vector<mint>(2, 0)));
    dp[0][0][0] = 1;

for (int i = 1; i <= n; i++) {
        for (int k = 0; k < i; k++) {
            for (int c = 0; c <= m; c++) {
                auto add = cnt[k+1][i];

for (int t = 0; t < 2; t++) {
                    if (c + add <= m) dp[i][c+add][t^1] += dp[k][c][t];
                }
            }
        }
    }

mint ans = 0;
    for (int i = 1; i <= n; i++) {
        for (int c = 1; c <= m; c++) {
            ans -= dp[i][c][0] * (mint(m) / mint(c));
            ans += dp[i][c][1] * (mint(m) / mint(c));
        }
    }

cout << ans << "\n";
}
```

## 杂题选讲
### 回文串有关的构造
#### Codeforces Round 1067 (Div. 2)
**[D. Palindrome Flipping](https://codeforces.com/contest/2158/problem/D)**
给定两个长度为`n`的串`s, t`，现在要求你通过不超过$$2n$$次的操作，把$$s \to t$$
一次操作如下，选择$$1 \leqslant l < r \leqslant n$$，满足$$s[l, r]$$是**回文的**
然后翻转`s[l, r]`所有的位，即`1 <--> 0`
要求构造方案，如果不可能，输出`-1`，每个方案输出两个数，分别是`l, r`
满足所有的$$O(n^2) \leqslant 5\cdot 10^5$$

**算法分析**
> 正着做很难做，能不能考虑构造一个中间字符串`tar`，使得`tar --> s,  tar --> t`
或者考虑将`s --> tar,  t --> tar`，因为操作是可逆的
只要能把`s --> tar`，再考虑将`t --> tar`**再反转操作**即可

全`0`或者全`1`串，任意子串都可以反转，与此同时，可以构造出任何想要的位
比如我们在全`0`串中，需要构造出`1`，那么只要**翻转后缀**`[i...n]`，然后再次翻转`[i+1...n]`即可

于是我们想，能不能将`s, t`都转换成全`0`或者全`1`串

> 将`[0 0 .... 0]`或者`[1 1 .... 1]`看作相同的块，压缩
因为这样的串，它的任意子串均可以完成翻转，均是合法的
我们每一段都找出极长的`[0 0 ... 0] or [1 1 ... 1]`的段
接下来只需要考虑如何处理`(0 1 0 1 0)，(1 0 1 0 1)`这两种`case`即可

```bash
case1:
形如 0 1 0 1 0，先考虑处理 [0 1 0]

op1:
(0 1 0 1 0)
(1 0 1 1 0)
op2:
(1 0 0 0 0)
这种状态下，可以通过最多 2 次操作，变成全 1 or 全 0 的段

也就是说，可以通过 2 次操作，将第一位取反，后面都变成 0，如下表示
(a b a b a) --> (a ^ 1) + (a a a a)
op1: 翻转 [0, 2]
op2: 找到第一个极长的 [a a a .. a] 段，将其翻转
```
根据上面的分析，形如`0 1 0 1 0`的段，可以通过最多`len - 1`次操作，变成`全 1 or 全 0`段
而`全 1 or 全 0`段，可以**压缩成**`1 or 0`，对于后续的段也是如此处理
这样下来，处理这样的段的操作次数，是$$O(\sum len)$$的

```bash
case2:
形如 1 0 1 0 1，先考虑处理 [1 0 1]

op1:
(1 0 1 0 1)
(0 1 0 0 1)
op2:
(0 1 1 1 1)

接着可以通过 1 次操作变成全 0 段，2 次操作变成全 1 段
这种情况是对称的
```

> 算法设计

考虑将`S`和`T`都变成全`0`的串，操作方案记为`A, B`，答案就是`A + rev(B)`
怎么变成全`0`串呢？

**只要这个串还不是全 0 串**
1.找到极长的形如`[1 1 .. 1] or [0 0 .. 0]`的块，直接翻转
每一次翻转，起到的效果，就是让这个块变得和它前面和后面的字符一样
换句话说，实际上是将**这样的块不断延长**，成为更长的`全 0 or 全 1`块
```bash
.... 1 [0 0 ... 0] 1 ....
.... 0 [1 1 1 ... 1 1] 0 ....
...
[全 0 块] -> [更长的全 1 块] -> [更长的全 0 块] -> .... ->
```

2.操作到最后，要么已经是`全 0 or 全 1`串，要么形如
```bash
case1: 1 00...0
case2: 0 11...1
```
而这种情况，只需要最多`2`次操作，就可以将其转为全`0`串

## Min-Max 容斥练习
**[E - Gachapon](https://atcoder.jp/contests/agc038/tasks/agc038_e)**
给定一个随机数生成器，它会生成$$0 \sim n - 1$$之间的整数，每个整数被生成的概率
由`a[0], a[1], ..., a[n-1]`给出，整数$$i \in [0, n - 1]$$被生成的概率是$$A_i / S$$

其中$$S = \sum\_{i = 0}^{n-1} a\_i$$，每次生成随机数是独立进行的
不断生成随机数，直到满足以下条件
对于所有的$$0 \leqslant i \leqslant n - 1$$，随机数生成器生成$$i$$的次数$$\geqslant B_i$$次

求操作的期望次数，期望对`998244353`取模

> Min-Max 容斥

如果$$i$$被生成的次数$$\geqslant B_i$$，我们称$$i$$这个元素**被满足**
根据 Min-Max 容斥
```math
\displaystyle
E(\max S) = \sum_{T \subseteq S} (-1)^{|T|+1} E(\min T)
```
其中$$\max S$$指的是集合中最后一个元素被满足的时间，$$\min T$$指集合中有元素**第一次被满足**的时间
**注意**，这里被满足，不仅仅是指生成，如果是单单生成$$i$$，概率是$$a_i / (\sum a_i)$$
比较麻烦的是，这里要求$$i$$至少被生成$$\geqslant B_i$$次

> 也就是说，这里不仅仅要求**命中**$$T$$，还必须**命中**$$T$$一定的次数
**进行多少次试验直到出现第 r 次成功**，这是一个**负二项分布**的问题

### 几何间隔
当我们只记录$$T$$上的抽取序列时，落在$$T$$的那几次抽取之间，会有若干次落在$$T^c$$的空白 gaps
每个 gaps 的长度是独立的，符合**几何分布**
`(上一次落在 T，下一次落在 T]`总的抽取次数的期望是$$\dfrac{1}{P}$$
上一次成功抽取结束（不包括上一次），到下一次成功命中$$T$$，这一段期望长度是$$\dfrac{1}{P}$$
```math
\displaystyle
E(XY) = E(X)E(Y) \\
E(T^c+T) = E(\dfrac{1}{P} T) = \dfrac{1}{P} E(T)
```
相当于每一次命中$$T$$，都需要**总的试验次数**是$$\times \dfrac{1}{P}$$倍

> 接下来只需要计算，满足$$T$$的期望时间
注意，这里命中和满足是不一样的，命中是指选到$$T$$中的元素
而满足的意思，是只考虑选$$T$$中的元素，但是要求存在$$i$$使得出现次数$$\geqslant b_i$$，所需要的抽取次数

**尾和公式**
记$$t$$为$$T$$第一次被满足的时间
```math
\displaystyle
E(T) = P(t = 1) + 2P(t = 2) + 3P(t = 3) + \cdots \\
= (P(t = 1) + P(t = 2) + P(t = 3) + \cdots) + (P(t = 2) + \cdots) + \cdots + \\
= P(t \geqslant 1) + P(t \geqslant 2) + \cdots
```
而注意到$$P(t \geqslant 1)$$可以如下改写
```math
\displaystyle
P(t \in [0, 0] \text{未满足}) + P(t \in [0, 1] \text{未满足}) + P(t \in [0, 2] \text{未满足}) + \cdots
```
记未满足状态下，每个元素出现次数为$$c\_0, c\_1, \cdots, c\_{m-1}$$（我们假定$$T$$中有$$m$$个元素）
而以上可以写成
```math
\displaystyle
\sum_{c_0, c_1, \cdots, c_{n-1}} \prod_{i \in T}P(c_i), \quad c_i \in [0, b_i-1] \\ = (\text{方案数}) \cdot  \prod_{i \in T}P(c_i)
```

方案数，假设有$$k$$次命中$$T$$的操作，那么就必须满足$$\sum c_i = k$$
```math
\displaystyle
\sum_{k = 0}^{\sum(b_i - 1)} \binom{k}{c_0, c_1, \cdots, c_{m}} \cdot \prod_{i \in T} P(c_i)
```
其中
```math
\displaystyle
P(c_i) = \left(\dfrac{a_i}{|T|} \right)^{c_i}
```
其中$$|T| = \sum\_{j \in T} a_j$$

化简，注意到$$|T|$$和$$i$$无关
```math
\displaystyle
\prod_{i \in T} \dfrac{1}{|T|^{c_i}} = \dfrac{1}{|T|^{\sum_{i \in T} c_i}} = \dfrac{1}{|T|^k}
```
综上所述，$$E(T)$$可以化简成
```math
\displaystyle
\sum_{k} \dfrac{k!}{|T|^k} \prod_{i \in T} \dfrac{a_i^{c_i}}{c_i!}
```
最终的答案要乘上一个系数$$\dfrac{1}{P}$$，令$$|S| = \sum\_{j = 0}^{n-1} a_j$$

```math
\displaystyle
P = \dfrac{\sum_{i \in T} a_i}{\sum_{j \in [0, n-1]} a_j} \\
\quad \\
\dfrac{1}{P} = \dfrac{|S|}{|T|}
```
从而
```math
\displaystyle
ans = |S| \sum_{T \subseteq S} (-1)^{cnt(T)-1} \cdot \sum_{k} \dfrac{k!}{|T|^{k+1}} \prod_{i \in T} \dfrac{a_i^{c_i}}{c_i!}
```
其中，$$cnt(T)$$表示$$T$$中有多少个元素

### 尾和公式+生成函数
记$$k$$为$$T$$第一次被满足所需要的操作次数，这里的操作包括选出$$\not \in T$$中的元素
```math
\displaystyle
E(\min T) = \sum_k k P(t = k) = P(t \geqslant 1) + P(t \geqslant 2) + \cdots \\
= \sum_{k = 0}^{+\infty} P([0, k] \text{均不满足})
```
那么$$k$$次中，假设说有$$t$$次命中$$T$$，有$$k - t$$次未命中，那么$$\sum\_{i \in T} c\_i = t$$
```math
\displaystyle
\sum_{k = 0}^{+\infty} \sum_{t \leqslant k} \dfrac{k!}{(k-t)! \prod_{i \in T}c_i!} \prod_{i \in T}p_i^{c_i} \cdot Q^{k - t} \\
\quad \\
= \sum_{k = 0}^{+\infty} \sum_{t \leqslant k} \dfrac{k!}{(k-t)!} Q^{k-t} \cdot \prod_{i \in T} \dfrac{p_i^{c_i}}{c_i!}
```
交换求和顺序，我们有
```math
\displaystyle
\sum_{t = 0}^{\sum(b_i - 1)} \left( \sum_{k = t}^{+\infty} \dfrac{k!}{(k-t)!}Q^{k-t} \right) \prod_{i \in T} \dfrac{p_i^{c_i}}{c_i!}
```
先考虑计算
```math
\displaystyle
\sum_{k = t}^{+\infty}\dfrac{k!}{(k-t)!}Q^{k-t} \xLeftrightarrow{k-t = m}  \sum_{m = 0}^{+\infty} \dfrac{(m+t)!}{m!}Q^{m} = t! \sum_{m= 0}^{+\infty}\binom{m+t}{m}Q^{m}
\\ = \dfrac{t!}{(1-Q)^{t+1}} = \dfrac{t!}{P^{t+1}}
```

> 最后一步化简，是基于**负二项的生成函数**来实现的
> 
```math
\displaystyle
\dfrac{1}{(1-x)^r} = (1-x)^{-r} = \sum_{k = 0}^{+\infty} \binom{r+k-1}{k}x^k \xLeftrightarrow{r-1 = t} \\
\quad \\
\dfrac{1}{(1-x)^{t+1}} = \sum_{k = 0}^{+\infty} \binom{t+k}{k}x^k
```

综上所述，最后的答案是
```math
\displaystyle
\sum_{t = 0}^{\sum(b_i - 1)} \dfrac{t!}{P^{t+1}} \prod_{i \in T} \dfrac{p_i^{c_i}}{c_i!}, \quad \sum_{i \in T} c_i = t, c_i \in [0, b_i-1]
```
不难发现，两种求解方法结果一样

### 动态规划计算
```math
\displaystyle
ans = |S| \sum_{T \subseteq S} (-1)^{cnt(T)-1} \cdot \sum_{k} \dfrac{k!}{|T|^{k+1}} \prod_{i \in T} \dfrac{a_i^{c_i}}{c_i!}
```
其中$$|T| = \sum\_{j \in T} a\_j, k = \sum\_{j \in T} c\_j$$，考虑每个数选 or 不选到$$T$$中
用$$dp(i, t, k)$$来计算，其中$$t$$表示$$|T|$$，枚举$$t, k$$，这样$$|T|, k$$确定的情况下
只有$$c_i$$是变化的，$$c_i \in [0, b_i - 1]$$
```math
\displaystyle
dp(i, t, k) = dp(i-1, t, k) - \sum_{c_i = 0}^{\min(k, b_i-1)} dp(i-1, t-a_i, k - ci) \cdot \dfrac{a_i^{ci}}{ci!}
```
dp 的初值呢？很显然是$$dp(0, 0, 0) = -1$$，`1-indexed`

最后的答案，就是$$\displaystyle |S| \sum\_{t = 0}^{|S|} \sum\_{k = 0}^{\sum (b\_i - 1)} \dfrac{dp(n, t, k)}{t^{k+1}} k!  $$

上一篇：十一月算法竞赛选题（二）下一篇：十二月算法竞赛选题（一）

看完文章有啥想法