十月算法竞赛选题（一）

[[ slider_text ]]

[[ item.c ]]

十月算法竞赛选题（一）

发布时间 2025-11-01 作者：秋千月 来源：算法小站

数据结构优化dp 博弈论 分块

## CodeTON Round 8
### C1
**[C1. Bessie's Birthday Cake (Easy Version)](https://codeforces.com/contest/1942/problem/C1)**
给定凸的$$n$$多边形，顶点编号是$$1 \sim n$$，现在选定一些点，问这些点能够连成多少个三角形
一共能选的点有$$x$$个
连成的三角形指的是三角剖分中，三角形的数量

**算法分析：关于三角剖分**
**结论1**
从$$n$$个顶点能画出的对角线总数（任意两个顶点可以相连，但不能算上原来的边）
```math
\displaystyle
\binom{n}{2} - n = \dfrac{n(n - 3)}{2}
```
任意取两个点构成$$\binom{n}{2}$$条线段，原来就有$$n$$条边，扣除，剩下都是对角线

**结论2**
把一个$$n$$凸多边形做三角剖分（用不相交的对角线，把多边形完全划分成三角形）
三角形的个数$$T = n - 2$$
用到的对角线数（每次剖分增加的对角线数）$$d = n - 3$$

> 结论 2 的推导

**直接统计**
假设剖分后有$$T$$个三角形，剖分对角线数是$$d$$，那么
三角形边的计数总和是$$3T$$，这些计数由原来的边$$n$$条，以及内部的对角线$$d$$构成
每条对角线计算了$$2$$次，所以$$3T = n + 2d$$

另一方面，把$$n$$边形划分成$$T$$个三角形，需要切割的次数，显然是一个对角线切一次
需要切$$T - 1$$次，所以$$d = T - 1$$，那么$$3T = n + 2(T - 1)$$

从而$$T = n - 2, d = n - 3$$

**递推**
用$$f(n)$$记$$n$$边形的三角剖分的**三角形个数**，注意到每一次可以找到相邻`3`个顶点构成的三角形
将其切去，剩下的又是一个子问题，对应$$f(n - 1)$$
从而有$$f(n) = f(n-1) + 1$$

递推的终点（首项）是$$f(3) = 1$$，根据等差数列递推，$$f_3 + (n-3)\cdot 1 = f_n$$，从而$$f_n = n-2$$

**欧拉公式**
欧拉公式的表达式是$$V - E + F = 2$$
其中，$$V$$是顶点数，$$E$$是边数，$$F$$是平面数

那么对应$$V = n$$，假设三角剖分形成$$d$$条对角线，那么$$E = n + d$$
面数呢？假设分成$$T$$个三角形，面数是$$F = T + 1$$，（最外部的平面也算一个面）

综上，有$$n - (n+d) + (T + 1) = 2$$，从而$$T = d + 1$$

另外，$$3T - d = E$$，因为每条三角剖分的对角线被多算了一次
所以又有$$3T - d = n + d$$，推出$$T = n - 2$$

> 再来考虑这个问题

如果$$x = n$$，那么答案就是$$x - 2$$
否则的话呢？答案最少是$$x - 2$$，再一些情况下，可能这个答案会增加，什么情况下答案会增加呢？

如果$$a[i] - a[i-1] > 2$$，那么你一定要选$$(i-1, i)$$，而$$[a\_{i-1}, a\_{i}]$$中间的点
一定都不会被选，不会有新的三角剖分产生

而如果$$a\_{i} - a\_{i-1} = 2$$，那么$$[a\_{i-1}, a\_{i}]$$中间还必然夹杂着一个点
这个点必然会构成一个三角剖分，那么这个点也要**作为必选点，考虑进去**
最终的答案是`(必选点的个数) - 2`

当然，注意是一个环形的，环的首尾，`a[1] - a[n] + n = 2`也单独存在一个合法点

### C2
**[C2. Bessie's Birthday Cake (Hard Version)](https://codeforces.com/contest/1942/problem/C2)**

**算法分析**
有了 C1 的结论之后，这种情况下，我们能够额外添加`extra`个点
考虑到对已有的点进行排序，每相邻两个点，`l = a[i-1] + 1, r = a[i] - 1`，那么$$[l, r]$$区间内的点都是未染色的

根据之前的分析，这些点如下进行类似二分图交错染色
如果是奇数
```bash
o -- x -- o -- x -- ... -- o -- x -- o

x 表示染色的点
```
那么这一整段都会变成**有效节点**，没有浪费

如果是偶数呢？
```bash
o -- x -- o -- x ... -- o -- x
```
会有一个浪费

那么我们贪心的思路就比较明显了，用一个二元组$$(d, [l, r])$$维护
按照$$d$$（间隔）从小到大染色

先处理`d = 奇数`，从小到大染色，然后再处理`d = 偶数`，从小到大染色
这样就不会有浪费了

### D
**[D. Learning to Paint](https://codeforces.com/contest/1942/problem/D)**
用一个`n`个格子组成的画布，编号从`[1...n]`，可以选择任意的格子染色
给定一个二维数组$$a$$，用来评价得分

对一个画布，其被涂色的**最大连续区间**是$$[l_1, r_1], [l_2, r_2], \cdots, [l_x, r_x]$$
画布的美丽度是所有的$$a[l_i, r_i]$$之和
```math
\displaystyle
\sum_{i = 1}^{x} a_{l_i, r_i}
```
一共有$$2^n$$种不同的染色方式，问最大的$$k$$个美丽值是多少？$$n \leqslant 10^3$$

**算法分析**
先考虑朴素的 dp，根据每个格子染色与否，可以设计出状态转移方程
```math
\displaystyle
dp_{i, 0} = \max(dp_{i-1, 0}, dp_{i-1, 1}) \\
dp_{i, 1} = \max_{0 \leqslant j \leqslant i-1} (dp_{j, 0} + a_{j+1, i})
```

关于第一个表达式，维护前$$k$$大很简单，实际上，这里的$$dp(i, 0), dp(i, 1)$$表示的并不是一个值
**而是一个大小最多为 k 的有序数组**，按照**从大到小**$$\geqslant$$排序
这样第一个方程的状态转移，等价于有序数组的**归并**

第二个表达式，如果按照$$\\{dp(j, 0) + a(j+1, i)\\}$$有序数组归并
对于每个$$i$$，代价都是$$O(nk)$$，整体的代价是$$O(n^2 k)$$，考虑优化

能够优化的点是，对于$$i-1 \to i$$，不用每次都`for j = 0 to i-1`，考虑能不能复用上一次求出来的$$dp(j, 0)$$的结果

**考虑堆优化**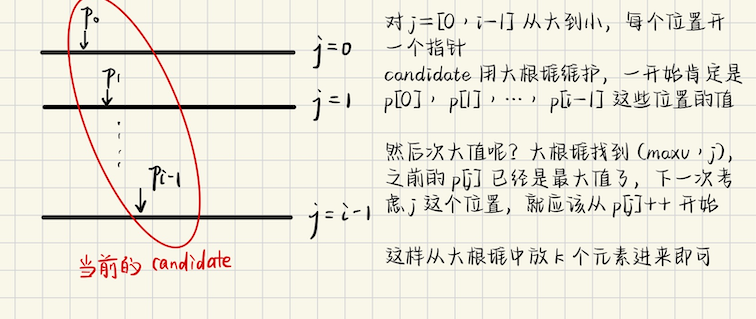
![](/media/content_img/codeton8-D.png)

### E
**[E. Farm Game](https://codeforces.com/contest/1942/problem/E)**
给定一个农场，可以抽象成边界是$$0, l+1$$，而$$[1, 2, \cdots, l]$$是空位
现在 FJ 和 FN 玩游戏，两个人都各自有$$n$$头牛，共$$2n$$头牛，他们把牛放到不同的整点上
并且 FN, FJ 各自的奶牛都互不相邻
要么是$$0 < a_1 < b_1 < a_2 < b_2 < \cdots < a_n < b_n$$
要么是$$0 < b_1 < a_1 < b_2 < a_2 < \cdots < b_n < a_n$$

一次移动，可以选择一个$$1 \leqslant k \leqslant n$$，以及一个方向
然后会选择$$k$$头牛向这个方向移动一个单位，不能把牛移动到墙上
或者另外一个玩家的牛上，如果一个人再也无法移动他的牛，他就输了，FJ 先手

给定$$l, n$$，保证$$n \leqslant l/2$$，问双方采用最优策略的情况下，FJ 能够赢的初始奶牛排列的方案数
当然了，有时候游戏会无穷无尽地继续下去，这时候算无人获胜

> 先来看简单情况

不妨假设$$a_i < b_i$$，那么如果$$\forall i, b_i - a_i = 1$$，即`a[i] b[i]`，这时候一定是**先手必败态**
因为先手只能往左走，后手跟着先手走，就一定可以堵住先手的位置

那么如果形如`a[i] _ b[i]`呢？那么`a[i]`先手可以考虑往右走一步，构成$$a_i < b_i$$且$$b_i$$先手的状态
这个时候对于`b`是**必败的**，也就是说，如果存在这个位置$$i$$，关于这个位置$$i$$
是**先手必胜的**

> 稍微复杂点

考虑形如`a[i] _ _ b[i]`这种情况呢？首先，`a[i]`和`b[i]`都往相同的方向移动是没有意义的
因为这样两者之间的**相对距离**并不会变化，最后总是会遇到`b[i]`不能和`a[i]`同方向的情况
（比如都往右，最后总会遇到`b[i]`不能继续再往右的情况）

只需考虑`a[i]`往右，`b[i]`往左的情况
这种情况下，`a[i] _ _ b[i]`可以经过变换，到达`a[i] b[i]`并且`a[i]`先手的状态
而这个状态是先手必败的

当然还有一种可能是`a[i] _ _ b[i]`，`a[i]`往右，`b[i]`不动，但不会选择这么做
因为这样就变成了`a[i] _ b[i]`，`a[i]`先手的情况，这种情况是先手必胜的，题目中保证了每个人都是最优策略
所以这种情况不会发生

综上所述，`a[i] _ _ b[i]`，`a[i]`关于`i`这个位置，**先手必败**

更进一步的，我们已经推出了$$b_i - a_i = 3$$是**先手必败**的状态，归纳地
可以推出$$b_i - a_i = \\{5, 7, 11, \cdots, 2k+1\\}$$也都是**先手必败**的状态
比如说$$b_i - a_i = 5$$的情况，已知`3`是先手必败态，当前的距离为`5`
那么我后手`b`，就可以采用和`a`**相向而行**的策略，到达`距离为 3，并且 a 先手的必败状态`

这样就可以得出第一个结论
如果所有位置$$i$$，都有$$b_i - a_i$$**是奇数**，那么一定是`a`先手必败

> 再看`a[i] _ _ _ b[i]`的情况，已知`a[i] _ b[i]`先手是`a`的先手必胜态

注意到，这个时候`a`先手，一定会转移到`a[i] _ _ b[i]`且`b[i]`先手的情况
这种情况，对于`b[i]`是一个先手必败态，那么轮到`b[i]`了，它要么不动`b[i]`，这个时候他是先手必败的
要么就是往左走，转移到`a[i] _ b[i]`且`a[i]`先手的情况，这种情况对于`a`，又是先手必胜状态

所以只要存在一个位置`i`，满足$$b_i - a_i$$**是偶数**，这个位置对于`a`就是**先手必胜**的

> 这样，答案就容易计算了

```bash
ans = 所有的方案数 - 每一对(a[i], b[i])都间隔了偶数个空位的方案数
```
总方案数是$$\displaystyle \binom{l}{2n}$$

而偶数个空位的方案数怎么算呢？
需要枚举所有牛之间的空位总和$$i \in [0, l]$$，并且$$i$$是偶数

先把对手`b`的$$n$$个位置确定下来，方案数是$$\displaystyle \binom{l - i - n}{n}$$
为什么呢？一共$$i$$个空位不能选，另外还需要$$n$$个位置留给`a`放置
剩下的位置可以随便选，选出$$n$$个位置来

接下来确定`a`，但是怎么保证每一对`(a[i], b[i])`之间有偶数个空位呢？
假设`(a[i], b[i])`之间有$$d$$个空位
```bash
a[i] _ _ ... _ _ b[i]

(a[i] _ _ _ 前 d/2 个空位) (后 d/2 个空位 _ _ _ b[i])
```
可以这么看，前$$d/2$$个空位，和$$a_i$$捆绑在一起，后$$d/2$$个空位，和$$b_i$$捆绑在一起
只需要确定每一个$$a_i$$后面，跟着几个空位就可以确定方案
假设说每个$$a_i$$后面跟着$$x_i$$个空位，$$x_i \geqslant 0$$
问题转化成$$x_1 + x_2 + \cdots + x_n = i / 2$$的**非负整数解**的方案数

这个方案数可以用插板法，或者不定方程正整数解的结论来求
答案是$$\displaystyle \binom{i/2 + n - 1}{n - 1}$$

综上所述，非法方案的答案是$$\displaystyle \binom{l - i - n}{n} \binom{i/2 + n - 1}{n - 1}$$

### F
**[F. Farmer John's Favorite Function](https://codeforces.com/problemset/problem/1942/F)**
定义$$f\_i = \sqrt{f\_{i-1} + a\_i}, f\_0 = 0$$，序列`a[1...n]`是给定的
有`q`次操作，每次操作单点修改一个$$a\_i$$值，每次修改后，询问$$\lfloor f\_n \rfloor$$的值

**算法分析**
> 定义$$g(i) = \lfloor f(i) \rfloor$$，那么有递推$$g(1) = \lfloor \sqrt{a_1} \rfloor, \quad g(i) = \lfloor \sqrt{g(i-1) + a_i} \rfloor$$

可以归纳法，对$$i$$归纳
假设$$g(i) = \lfloor f_i \rfloor$$，那么有
```math
\displaystyle
\lfloor f_{i+1} \rfloor = \lfloor \sqrt{f_i + a_{i+1}} \rfloor = \lfloor \sqrt{f_i - \delta + a_{i+1}} \rfloor \ (0 \leqslant \delta < 1)
```
为什么呢？因为$$\delta$$是小数，减去后不影响**下取整**
如果要严格说明的话，$$\lfloor x \rfloor = x - \delta$$，那么有$$x - 1 < x - \delta \leqslant x$$
```math
\displaystyle
\lfloor f_{i+1} \rfloor = \lfloor \sqrt{\lfloor f_i \rfloor + a_{i+1}} \rfloor = \lfloor \sqrt{g_i + a_{i+1}} \rfloor = g_{i+1}
```

> 考虑 $$f\_{i} = \sqrt{ f\_{i-1} + a\_i }$$ 的收敛性

如果分块，假设说当前块的区间是$$[l, r]$$，当$$[l, r]$$足够长的时候，就进行了足够多次的根号运算
假设说已经求出了上一个块的值$$f\_{l-1}$$，那么修改$$a_l$$，递推
```math
\displaystyle
a_l \to old \\
a_l + 10^{18} \to new
```
可以推出，$$new - old \leqslant 1$$，这是为什么呢？
```math
\displaystyle
f_i = \sqrt{f_{i-1} + a_i + \Delta} = \sqrt{\sqrt{f + \Delta}} = \cdots
```
这样的操作可以使得$$\Delta \to 0$$，$$f$$的变化最多是`1`

> 于是可以初步设计算法

当块的长度$$[l, r] < B$$的时候，直接暴力计算这个块中每一个位置的值
否则我们需要预处理一些信息

假设当前考虑的块的编号是$$i$$，对应的区间是$$[L_i, R_i]$$
我们发现，即使是从$$\Delta = 0 \to 10^{18}$$，在经过$$10$$次的根号迭代后，$$\Delta \leftarrow \sqrt{\Delta}$$
最后有$$\Delta = 1$$

这个说明什么呢？说明即使是$$f\_{l-1} = 0$$，之前经过若干次修改之后，有$$f\_{l-1} = 10^{18}$$
即使是这样，经过块$$[l, r]$$运算完，最终的$$f\_{r}' - f\_r \leqslant 1$$，最多差`1`

假设说$$f\_{l-1} = 0$$时候，求出来$$res = f\_r$$，在$$f\_{l-1}< ?$$，**小于某个 threhold 阈值**的情况下
这时候求出来的$$f_r = res$$，都是$$res$$，**记`expect[i] = res`**

直到$$f\_{l-1}\geqslant ?$$，**大于等于 threhold**，$$f\_{r} = res + 1$$，除此之外不会有别的值

这样我们可以跳过块中的暴力计算，直接维护出来

> 那么我们需要预处理算出每个块的 threhold

对于块$$i, [l, r]$$，计算出$$f\_{l-1} = 0$$时候，能够得到的$$f\_r$$的值`res`
当$$<$$ **threhold**的时候，不管$$f\_{l-1}$$是什么数，算出来的都是`f[r] = res`

怎么求`threhold`呢？我们知道$$f\_{l-1} = $$**threhold**的时候，算出来的`f[r]`理应是`res + 1`
那我们就倒着递推，根据递推表达式$$f\_{i-1} = f\_{i}^2 - a\_i$$
这样从$$f\_{r} = res$$倒着递推一遍，就得到了`threhold[i]`

> 主算法就很简单了

对于每个询问，如果块长度$$\geqslant B$$，那么直接根据预处理维护的信息
跳过这个块，$$O(1)$$地得到走完整个块，$$f$$的值变成多少

那么我们从$$v = 0$$作为起点，开始算
对于块`i`，如果`v < threhold[i]`，答案就是`expect[i]`，否则的话，答案是`expect[i] + 1`

当然最后的块可能不满`B`的长度，这时候暴力计算即可

### G
**[G. Bessie and Cards](https://codeforces.com/contest/1942/problem/G)**
你有`a`张`0`类卡，`b`张`1`类卡，`c`张`2`类卡，`5`张特殊卡
现在随机排成一堆后，**每一轮**你从上面摸`5`张卡，每次打出一张`x`类卡，并且再摸`x`张卡
但你不能打出特殊卡

求集齐特殊卡的概率

**算法分析**
首先$$b$$是没有用的，因为等价于你抽到`b`就扔掉，重新开始抽
所以实际上就只有$$(a + c + 5)$$这么多卡，总的方案数是
```math
\displaystyle
\dfrac{(a+c+5)!}{a!c!5!}
```

> 接下来考虑集齐特殊卡的方案数，特殊卡可以看作`0 类`卡

这个过程可以看成这样，如果抽到`2 类`卡，你需要再抽一张，假设你一共抽了$$x$$张`2 类`卡
那么你就一定有$$x$$张`0 类`卡，而你抽到这些`0 类`卡的时候，是不能继续抽的
要求是这些`0 类`卡中，必须包含$$5$$张特殊卡

那么问题转化成，抽到`2 类`卡`+1`，抽到`0 类`卡`-1`，要求到终点前，任意时刻前缀和$$\geqslant 0$$

**分为两类**，即取完所有的卡，或者是**枚举**恰好取了多少张卡

> 先来看恰好取了一部分卡的情况

几个性质
1.抽到`2 类`卡，一定会匹配上**相应数量**的`0 类`卡
2.抽卡终止，当且仅当`2 类卡的数量 = 0 类卡的数量`，并且**最后一次抽**的一定是`0 类`卡
3.抽`2 类`卡看作`(`，抽`0 类`卡看作`)`，抽卡终止，前缀和恰好为`0`，并且中间的任何位置，前缀和$$\geqslant 0$$
4.类似括号匹配问题，`2 类 +1， 0 类 -1`
5.还有一个简化的性质，你后续抽到的`0 类`卡，它一定是由`2 类`卡**换来的**

用`(0类卡数量， 2类卡数量) =`$$(x, y)$$，这样的二元组表示状态
结束时候的状态，假设说我们后续抽到了$$x$$张`2 类`卡，那么终止状态是$$\Delta = (x+5, x)$$
其中$$x+5$$表示一定包括了`5`张特殊卡

由于最后一步是确定的，一定拿的是`0 类`卡，实际上终点$$x, y$$分别增加了多少呢？
那么$$\Delta_x = x+4, \Delta_y = x$$

实际上，题目中规定**一开始可以摸 5 张卡**，相当于你在初始状态有`5 张 2 类卡`
其中最后一张`2 类卡`，要被用于**最后一次抽卡**，来换一张`0 类`卡，结束抽卡过程
所以起点是$$(0, 4)$$

这样，问题转化成从$$(0, 4) \to (x+4, 4+x)$$有多少条路径，要求路径可以碰到$$y = x$$
但不能穿过$$y = x$$

> 这样做会不会漏解？其实不会，因为我们算的是方案数，假设说极端情况，我们一开始抽的`5`张都是特殊卡呢？
那么这时候对应的$$x = 0$$，$$(0, 4) \to (4, 4)$$恰好一条路径，那就是这`4`个`( ( ( (`
都必须安排`) ) ) )`，即`0 类卡`，并且这些`0 类卡`还必须是**特殊卡**

**问题转化**
实际上考虑一开始给定序列`( ( ( (`，要求构造合法的括号序列，并且`) ) ) ... )`中
恰好有`4`个`)`是染色成**特殊卡**的

记方案数是$$f(x, y)$$，表示从$$(0, 4) \to (x, y+4)$$有多少条合法路径，合法路径要求
可以碰到$$y = x$$，但是不能穿过$$y = x$$
每次只能向上走或者向右走，但注意，如果恰好碰到了$$y = x$$，就意味着`0 类卡和 2 类卡恰好抵消了`
下一步一定是往上走，拿`2 类卡`，不能继续拿`0 类`卡了，要求路径始终在$$y = x$$的上方

其中，$$(0, 4) \to (x, y+4)$$的总的方案数是$$\displaystyle \binom{x+y}{y}$$

每一个不合法的方案，相当于将$$y = x$$往下平移一个单位，即$$l': \quad y = x - 1$$
令$$(x, y+4)$$关于$$l'$$**对称**，对称点是$$(y+5, x-1)$$

不合法的方案，对应$$(0, 4) \to (y+5, x-1)$$路径的方案数，答案是$$\displaystyle \binom{x+y}{y+5}$$

综上所述
```math
\displaystyle
f(x, y) = \binom{x+y}{y} - \binom{x+y}{y+5}
```

> 路径方案数求出来了，下面构造合法的解，就是如何在`0 类`卡中，分配特殊卡？

首先，要在$$x+5$$个`)`中选`5`个位置，染色成特殊卡，方案数是$$\displaystyle \binom{x+5}{5}$$
另外，实际上，这个过程我们抽了$$x+5$$张`0 类卡`，$$x$$张`2 类卡`
也就是说，$$\Delta = 2x$$张**非特殊卡**，还剩下$$a + c - 2x$$张卡我们未动
这些卡中，我们仍然要分出`0 类卡，2 类卡`，那么这些卡中有$$a - x$$张`0 类卡`，$$c - x$$张`2 类卡`
所以最后，还应该乘上$$\displaystyle \binom{a+c-2x}{a-x}$$

综上所述，枚举$$x = [0\cdots \min(a, c)]$$，$$f(x+4, x)\cdot \displaystyle \binom{x+5}{5} \cdot \binom{a+c-2x}{a-x}$$

> 那么全部抽完的方案数呢？

答案是$$\displaystyle f(a+5, c) \cdot \binom{a+5}{5}$$

当然这是有前提的，要求`(`的总个数$$\geqslant$$`)`的总个数
也就是说`2类卡的总个数 >= 0类卡包括特殊卡的总个数`，包括一开始的`( ( ( ( (`
```bash
int s0 = a + 5, s2 = c
must:		s2 + 5 >= s0
```
这样才能取完所有的卡

#### 疑问

> 有个疑问，对于取完所有的卡的情况，all in 所有的卡
这个时候为什么起点仍然是$$(0, 4)$$，对应`( ( ( (`，计算出$$f(a+5, c)$$
而不是以$$(0, 5)$$作为起点，对应`( ( ( ( (`，再重新计算呢？

实际上，如果以`( ( ( ( (`作为起点，有可能取完所有的卡之后，构成的序列形如
```bash
( ( ( ( ( ...... () ... ()
```
即抽完所有卡之后，整个序列的前缀和恰好为`0`（因为统计方案的时候，只统计不跨越$$y = x$$）
点落在直线$$y = x$$上的时候，前缀和恰好为`0`，而这种情况，我们在第一部分**已经讨论过了**
再计算会重复

实际上，第一部分计算的就是在任何位置结束（包括抽完所有的卡，在整个序列结尾），前缀和恰好$$= 0$$的情况
而我们漏解的情况，恰恰是可能`2 类卡`特别多，导致在序列的结尾，前缀和会$$\geqslant 1$$的情况

怎么保证算到最后前缀和$$\geqslant 1$$呢？
我们从`( ( ( (`，即$$(0, 4)$$作为起点走，不穿越$$y = x$$，这样就能保证**中间过程**
前缀和一定是$$\geqslant 0$$的
然后再在序列的末尾补上一个`(`，这样就可以保证前缀和$$\geqslant 1$$了
所以仍然是从$$(0, 4)$$开始，取完所有的卡，对应的方案$$f(a+5, c)$$

上一篇：九月算法竞赛选题（四）下一篇：十一月算法竞赛选题（一）

看完文章有啥想法