九月算法竞赛选题（四）

[[ slider_text ]]

[[ item.c ]]

九月算法竞赛选题（四）

发布时间 2025-10-12 作者：秋千月 来源：算法小站

单调栈 dp计数

## 牛客小白月赛121
### D
**[D-谁敢动资本的蛋糕](https://ac.nowcoder.com/acm/contest/117762/D)**
给定`a[1...n]`，每次操作任意选择两个下标`i, j`，将$$a_i, a_j$$删掉，用$$a_i \oplus a_j$$来替换
代价是`2(a[i] & a[j])`，现在问，总代价的和最小是多少？

**算法分析**
利用恒等式
```math
\displaystyle
x + y = (x \oplus y) + 2(x \textbf{ and }  y)
```

总代价是不变的，$$\sum a_i - \bigoplus a_i$$

### E
**[构造序列](https://ac.nowcoder.com/acm/contest/117762/E)**
问构造长度为$$n$$的序列的方案数，每个数$$1 \leqslant a_i \leqslant m$$，另外，还必须满足，序列是好的
序列是好的，定义如下，能够将序列划分成若干连续的段，每个段中的元素都相等，并且任意相邻段颜色不相等
划分成连续的段有要求，假设划分成`k`段，每一段长度是$$l_1, l_2, \cdots, l_k$$，必须满足$$l_1 < l_2 < \cdots < l_k$$
问构造序列的方案数

**算法分析**
如果我们知道了划分成$$k$$段，那么相当于给每一段染色，相邻的段不能染同样的颜色
第一段有`m`种选择，第二段有`m-1`种，第三段呢，还是`m-1`
染色的方案数是$$m \cdot (m-1)^{k-1}$$
最后的答案是$$\sum_k ways(k) \cdot m(m-1)^{k-1}$$

> 下面考虑，把$$n$$划分成$$k$$个，**严格单调增**的数的方案

这是一个整数划分问题，假设说考虑前$$i$$个数，划分成了$$k$$段，每一段的长度都比前一段**严格单调增**
同时，不能用空段，这样的方案数记为$$dp(i, k)$$

> 如果划分的段的长度包含`1`

那么我们考虑**每一段都减去 1 个最小的数**，不难发现，这时候只有$$k-1$$段了，那个长度为`1`的段变空了
这个时候总共有几个数呢？一共有$$i - k$$个数
所以方案数是$$dp(i-k, k-1)$$

> 如果划分的段的长度不包含`1`

那么每一段都减去一个数，还是对应有$$k$$段，但是还剩下$$i - k$$个数，方案数是$$dp(i-k, k)$$

所以递推是$$dp(i, k) = dp(i-k, k-1) + dp(i-k, k)$$

## CodeTON Round 7
### G
**[G. Pepe Racing](https://codeforces.com/contest/1896/problem/G)**
有$$n^2$$个人，编号分别是$$1, 2, \cdots, n^2$$，速度两两不同
现在一次询问可以任意选`n`个人，你只会知道，速度最快的那个人的编号
问是否有可能在$$2n^2 - 2n + 1$$次的询问，确定速度最快的$$n^2 - n + 1$$的人
按速度从大到小排序即可，速度最慢的$$n-1$$个人没有必要区分开来

**算法分析**
> 如何确定速度最快的那个人？

分块，`[1, n] [n+1, 2n] [2n+1, 3n] .... [(n-1)n+1, n*n]`，对于第$$i$$块，范围$$[(i-1)n+1, in]$$
这样，分别对每一块进行查询最大值，耗费`n`次询问，得到一个长度为$$n$$的序列
记为$$b_1, b_2, \cdots, b_n$$，再针对`b[...]`进行一次最大值查询，也就是说$$n+1$$次查询，确定最大值

> 暴力怎么做？

顺着这个思路，自然而然想到，耗费$$n$$次确定序列`b[...]`，然后接下来的查询都是针对`b`的
怎么查询次大值呢？

1.需要知道最大值`mx`在的那个块的编号`idx`，不妨叫**被删块**
2.去`block[idx]`中把`mx`删掉，然后再从其他编号$$\neq idx$$的块中，选一个**非该块最大值，没选过的**元素
插入到**被删块**中
3.针对被删块，`b[idx]`，询问一次最大值，更新`b[idx]`，然后呢？再一次对全局的`b[1...n]`做一次询问
这样就能确定次大值

```bash
1次 查询，确定最大值 r[N]
接下来，次大值到目标，确定一个值需要 2 次询问
```
总的询问次数是，确定最大值，需要$$n + 1$$次询问，接下来还需要确定$$n^2 - n$$个人
每个人需要$$2$$次询问，总的询问次数是$$(n+1) + 2(n^2 - n) = 2n^2 - n + 1$$次，多了$$n$$次

> 怎么优化掉$$n$$？考虑后面的若干询问，能不能不要`2`次，而是只问一次？

也就是说，`2`次的询问，不能问太多，原来针对$$(n^2 - n)$$个数，现在看下$$(n^2 - n - n = n^2 - 2n)$$个数行不行

> 在重新分析一下

首先，分块进行$$n$$次操作，确定数组`b[1...n]`是必不可少的，接下来每确定一个排名，需要`2`次操作
```bash
1 次操作针对 b[1...n] 全局询问，确定当前第 k 大

第 2 次操作，确定 kth number 所在的块的 idx，然后 block[idx] 删去 kth
从非被删块（其他块），找一个不是最大值的，没被选过的数，补充到 idx 这个块中
花费一次操作，更新 b[idx]
```
如上所示，确定一个排名，需要一次全局询问，一次**补充更新**，`2`次操作
一次需要排名$$n^2 - n + 1$$个人，原来一个排名要`2`次询问，现在要节省出$$n$$次询问
说明**恰好有$$n$$个人，只需要`1`次询问确定排名**，剩下的$$n^2 - 2n + 1$$个人仍然是`2`次询问

换句话说，$$n + 2(n^2 - 2n + 1) + (n - 1)$$
另外，**被选为块内最大值的数**，需要标记（最大值标记）

> 数形结合考虑这个表达式

![](/media/content_img/CodeTon7G.png)

注意到`[n, 2n-1]`一共有`n`个数，也就是说，我们要迭代`n`次
每次操作，之前都是需要**全局查询一次**确定第`k`大，然后再更新`b[idx]`

直接确定$$[2n-1 \to n]$$的排名难度很大，每确定一个名次需要`2`个询问，能不能转而考虑$$[n-1\to 1]$$
实际上，对于**最后的**$$2n - 1$$个数，可以考虑**只全局查询最大值，不进行块更新询问**

> 我们期望的是

迭代`n-1`次，每一次只针对全局的`b[...]`查询最大值，因为**所有的数都两两不同**
1.查询完之后，删除当前`kth number`，删除前，记得**打上最大值标记**
2.然后呢，暴力地找**没有打上最大值标记**的数，添加到全局的`b[...]`中，直到`b[...]`长度恰好是`n`

这样可以吗？注意到剩下的数一共有$$2n - 1$$个，而仍然有`b[1...n]`，$$n$$个块
说明每个块中都有`2`个元素，恰好有一个块中仅有`1`个元素
注意到**之前，我们把选为块内最大值的数都标记了**
```bash
块中的元素情况如下
(max[1], ?), (max[2], ?), ...., (max[n-1], ?),  (maxn, )
```

块中的元素情况如上，迭代`n - 1`次，一定可以筛选出**接下来第`[1~n-1]`大的元素**
那最后还剩下一个元素，它肯定是被**最大值标记的**，直接暴力找到它即可

### 算法实现
```bash
void solve(int cas) {
    int n;
    cin >> n;

auto query = [&](const set<int> &ids) -> int {
        if (ids.size() == 0) return -1;

cout << "? ";
        for (auto x : ids) cout << x << " ";
        cout << "\n";
        cout.flush();

int x;
        cin >> x;
        return x;
    };

auto out = [&](const vector<int> &ans) -> void {
        cout << "! ";
        for (auto x : ans) cout << x << " ";
        cout << "\n";
        cout.flush();
    };

vector<set<int> > raw;
    int x = 1;
    for (int i = 1; i <= n; i++) {
        set<int> st;
        for (int j = 1; j <= n; j++) {
            st.insert(x), x++;
        }
        raw.emplace_back(st);
    }

// totmax
    vector<int> ans;
    vector<int> bmax(n, 0);
    map<int, int> mark;
    for (int i = 0; i < n; i++) {
        auto val = query(raw[i]);
        bmax[i] = val, mark[val] = 1;
    }

// [n^2...2n]
    int N = n * n;
    using pint = pair<int, int>;

auto queryBlk = [&]() -> pint {
        set<int> st;
        for (int i = 0; i < n; i++) st.insert(bmax[i]);
        auto totmax = query(st);

int bid = -1;
        for (int i = 0; i < n; i++) {
            if (bmax[i] == totmax) bid = i;
        }

return make_pair(totmax, bid);
    };

auto Fill = [&](set<int> &st) -> void {
        int val = 1;
        while (st.size() < n) {
            while (st.contains(val) || mark.contains(val)) val++;

st.insert(val);
        }
    };

auto upd = [&](int bid) -> void {
        auto nmax = query(raw[bid]);

bmax[bid] = nmax, mark[nmax] = 1;
        
        for (int i = 0; i < n; i++) if (i != bid) {
            raw[i].erase(nmax);
        }
    };

for (int i = N; i >= 2 * n; i--) {
        auto [totmax, bid] = queryBlk();
        ans.emplace_back(totmax);

raw[bid].erase(totmax), Fill(raw[bid]);

upd(bid);
    }

set<int> blkmx;
    for (int i = 0; i < n; i++) blkmx.insert(bmax[i]);
    Fill(blkmx);

for (int i = n-1; i >= 1; i--) {
        auto mx = query(blkmx);
        ans.emplace_back(mx);

blkmx.erase(mx), mark[mx] = 1;
        Fill(blkmx);
    }

for (auto x : blkmx) if (mark.contains(x)) ans.emplace_back(x);

out(ans);
}
```

## Codeforces Round 1055
### A
**[A. Increase or Smash](https://codeforces.com/contest/2152/problem/A)**
**问题描述**
给定一个长度为 n 的序列，一开始每个元素都是 0，现在可以任意顺序，任意次数执行以下两种类型的操作
第一，将所有的元素，都`+ 任意正整数 x`
第二，选择任意的元素，可以不选，将这些元素都变成`0`
将这个序列，变成目标序列`a`，需要最小的操作次数

**算法分析**
不难发现，只有`2`个元素的情况下，答案是`3`，考虑`3`个元素呢？
```math
\displaystyle
(a_1, a_2, a_3) \xleftarrow{+a_1} (0, a_2-a_1, a_3-a_1) \\
\xleftarrow{?}(?, x, y)
```
其中$$x = a_2 - a_1, y = a_3 - a_1, ?$$任意，换句话说，每多一个元素，需要多耗费`2`次操作
一次在相应的位置变`0`，再来一次变成目标元素

所以答案是$$3 + 2(m - 2) = 2m-1$$，其中$$m$$是有几个不同的元素

## Codeforces Round 904 (Div. 2)
### C
**[C. Medium Design](https://codeforces.com/contest/1884/problem/C)**
给定一个长度为$$m$$的序列`a[1...m]`，给定$$n$$个两两不同的区间$$1 \leqslant l_i \leqslant r_i \leqslant m$$
需要从这些区间中任选一个子集（可以是空集），进行如下操作
对于每个$$i = 1, 2, \cdots, n$$，如果区间$$(l_i, r_i)$$被选入子集，那么将$$[l_i, r_i]$$区间内的所有数
都加上`+1`
如果区间没有被选中，那么数组不变
处理完所有的数之后，区间的代价定义为，$$\max(a) - \min(a)$$，最大化这个代价

**算法分析**
首先能够分析出来，最优的代价一定是会留着一个`0`，然后最大值位置被尽可能多的线段覆盖
那么很直接的一个思路，枚举`0`的位置在哪里，同时区间查询最大值

可以考虑**一开始把所有的区间都加进来**，然后枚举`i`这个位置取到`0`，把所有覆盖到$$i$$这个点的线段都删掉
查询全局最大值，查询完之后把删掉的线段再还原现场，加回来，继续下一个位置

具体来说，可以用双指针，$$i, j$$
先按左端点从小到大排序，再考虑按右端点从小到大排序，枚举`0`的位置$$p$$

首先，对于$$[l_i, r_i]$$，$$l_i > p$$的区间已经被加进来了，不用管，$$l_i \leqslant p$$的区间都删掉
但是有可能多删了，满足$$r_j < p$$的区间$$[l_j, r_j]$$就被多删了，把这样的区间加回来即可

处理完之后，查询`[1, m]`的最大值即可

### D
**[D. Counting Rhyme](https://codeforces.com/contest/1884/problem/D)**
给定一个长度为`n`的序列`a`，$$(i, j)$$是好的对，当且仅当**不存在**任何一个$$k$$使得$$a_k \mid a_i$$并且$$a_k \mid a_j$$
问好对的数量

**算法分析**
如果$$(i, j)$$是好对，当且仅当$$\forall k, a_k \nmid \text{gcd}(a_i, a_j)$$，这种问题可以考虑枚举`gcd`
转换成类似**数论函数**一样的形式，定义
```math
\displaystyle
f(d) = \begin{cases} 0 & \exists i \in [1, n], a_i \mid d \\
1 & \forall i \in [1, n], a_i \nmid d \end{cases}
```
这样好对的数量，就是
```math
\displaystyle
\sum_{i = 1}^{n} \sum_{j=i+1}^{n} f(\text{gcd}(a_i, a_j))
```
这种形式，都是考虑**枚举 gcd**
```math
\displaystyle
\sum_{g = 1}^{n} f(g) \sum_{i = 1}^{n}\sum_{j=i+1}^{n} [\text{gcd}(a_i, a_j) = g]
```

其中，$$\sum f(g)$$很好求
```bash
for ai = 1 to n（注意，ai 要在序列中出现过）
		枚举 ai 的倍数，f( ai 的倍数 ) = 0
```

下面考虑有多少对$$(i, j), i < j$$，满足$$(a_i, a_j)$$的`gcd = g`，可以用**狄利克雷后缀**
先预处理出$$g \in [1, n]$$，`g`的倍数有多少个呢？记为$$cnt(g)$$
```math
\displaystyle
dp(g) = \binom{cnt_g}{2} - dp( g \text{ 的倍数} )
```
这里从`g = n downto 1`倒着`for`一遍，即可求出

### E
**[E. Hard Design](https://codeforces.com/contest/1884/problem/E)**
给定一个整数数组`b[0], b[1], ....., b[n-1]`，你的目标是使得所有元素都相等，可以进行若干次如下操作
第一，选择一对下标$$0 \leqslant l \leqslant r \leqslant n-1$$，对于每个$$i \in [l, r]$$，将$$b_i + 1$$
第二，每一次这样的操作，获得$$(r-l+1)^2$$个金币

定义$$f(b)$$是一个整数对$$(cnt, cost)$$，`cnt`是将数组所有元素变成相等的，所需要的最少操作次数
`cost`表示在所有能用`cnt`次操作完成目标的方案中，能获得的最大金币数
最小化`cnt`，`cnt`相同的时候，最大化`cost`值

现在给定一个序列$$a\_0, a\_1, \cdots, a\_{n-1}$$，对于`a`的所有循环移位，求出`f`的值
对于每个$$i = 0, 1, \cdots, n - 1$$，执行以下操作

令$$c\_j = a\_{(i+j) \bmod n}$$，其中$$0 \leqslant j \leqslant n - 1$$，求出$$f(c)$$
比如`[1, 3, 2]`，你需要求出$$f([1, 3, 2]), f([3, 2, 1]), f([2, 1, 3])$$

**算法分析**
> 结论题，给定一个正整数序列，一次操作任选$$(l, r)$$，使得$$[l, r]$$中的数全部都`-1`，不允许出现负数
问将序列变成`0`至少需要几次操作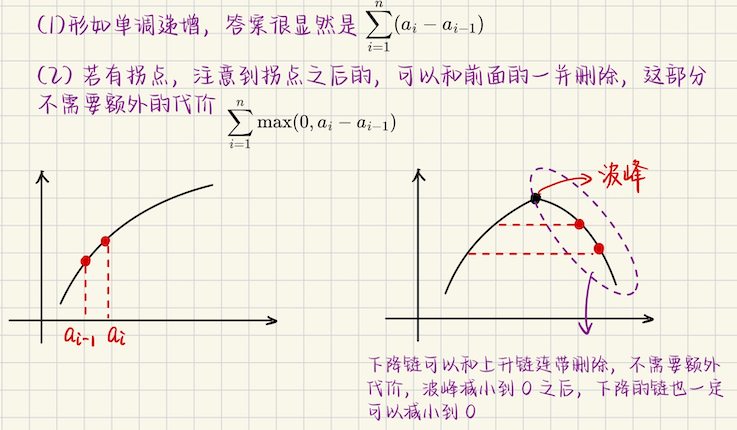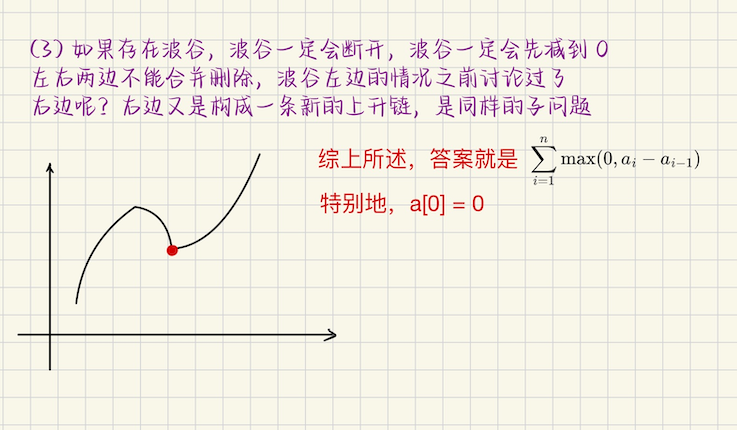
![](/media/content_img/cf904e1.png)
![](/media/content_img/cf904e2.png)

那么求`cnt`，可以令$$a_i = maxv - a_i$$，这样更改定义之后，答案就是将$$a_i$$变成`0`所需要的最小代价

答案就是$$\sum \max(0, a\_i - a\_{i-1})$$

> 接着考虑循环移位怎么做呢？

对于`cnt`，不难想到破环成链，复制一倍，求$$i$$为起点的`cnt`，实际上是求$$i \sim i + n - 1$$
可以利用前缀和，求出`sum( a[i+1]-a[i],  a[i+2]-a[i+1], ...., a[i+n-1]-a[i+n-2] )`，即$$S(i+n-1) - S(i)$$
最后再加上从$$0 \to a_i$$的代价
所以$$cnt(i) = S(i+n-1) - S(i) + a_i$$

> 难点在于`cost`怎么求

![](/media/content_img/cf904e3.png)
![](/media/content_img/cf904e4.png)

**算法实现**
```bash
void solve(int cas) {
    int n;
    cin >> n;

vector<i64> raw(n+1, 0);
    for (int i = 1; i <= n; i++) cin >> raw[i];

auto N = 3 * n;
    vector<i64> a(N+1, 0);
    for (int i = 1, j = 1; i <= n; i++, j++) a[i] = raw[j];
    for (int i = n+1, j = 1; i <= 2 * n; i++, j++) a[i] = raw[j];
    for (int i = 2*n+1, j = 1; i <= N; i++, j++) a[i] = raw[j];

i64 maxv = *max_element(a.begin()+1, a.end());

int p = 0;
    for (int i = 1; i <= 2 * n; i++) if (a[i] == maxv) p = i;

assert(n <= p && p <= 2 * n);
    // debug(make_pair(p, maxv));

for (int i = 1; i <= N; i++) a[i] = maxv - a[i];

// debug(a);
    vector<i64> s(N+1, 0);
    for (int i = 1; i <= N; i++) {
        s[i] = s[i-1] + max(0LL, a[i] - a[i-1]);
    }

vector<i64> anscnt(n+1, 0);
    for (int i = 1; i <= n; i++) {
        anscnt[i] = s[i+n-1] - s[i] + a[i];
    }

using pint = pair<i64, i64>;
    // (val, cnt)
    vector<mint> ri(N+5, 0), le(N+5, 0);

stack<pint> stk;
    mint sum = 0;

// debug(p);
    for (int i = p+1; i <= p+n; i++) {
        i64 cnt = 1;

while (stk.size() && stk.top().first >= a[i] ) {
            auto [top, lastcnt] = stk.top();
            stk.pop();

sum -= mint(lastcnt) * mint(top - a[i]);
            cnt += lastcnt;
        }

int d = i - p;
        ri[d] = ri[d-1] + mint(2) * sum + mint(a[i]);
        sum += a[i];

stk.push(pint{a[i], cnt});
    }

while (stk.size()) stk.pop();
    sum = 0;

for (int i = p-1; i >= p-n; i--) {
        i64 cnt = 1;

while (stk.size() && stk.top().first >= a[i]) {
            auto [top, lastcnt] = stk.top();
            stk.pop();

sum -= mint(lastcnt) * mint(top - a[i]);
            cnt += lastcnt;
        }

int d = abs(i - p);
        le[d] = le[d-1] + mint(2) * sum + mint(a[i]);
        sum += a[i];

stk.push(pint{a[i], cnt});
    }

vector<mint> ans(n+1, 0);

for (int i = 1; i <= n; i++) {
        int l = p - i, r = n - 1 - l;
        l = safeMod(l, n), r = safeMod(r, n);

ans[i] = le[l] + ri[r];
    }

for (int i = 1; i <= n; i++) {
        cout << anscnt[i] << " " << ans[i] << "\n";
    }
}
```

上一篇：九月算法竞赛选题（三）已经是最后一篇啦

看完文章有啥想法