算法小站
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
登录
注册
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
七月算法竞赛选题(二)
差分,最长回文路径,回文,多重集的排列,换根,哈希,环上统计 .....
[[ slider_text ]]
[[ item.c ]]
0
0
七月算法竞赛选题(二)
发布时间
2025-07-23
作者:
秋千月
来源:
算法小站
树上问题
排列与置换
## AtCoder Beginner Contest 414 ### D **[D - Transmission Mission](https://atcoder.jp/contests/abc414/tasks/abc414_d)** **问题描述** 给定$$n$$个点,要求恰好用$$m$$个区间,将所有点完全覆盖,每个区间的代价是$$|r - l|$$ 要求使得**覆盖的代价和**最小 **算法分析** 这个问题用$$dp$$,方程似乎很好写 ```math \displaystyle dp(i, k) = \min_{j < i} dp(j, k-1) + (a_i - a_{j+1}) ``` 这种后面的方程,和$$i$$有关又和$$j$$有关,考虑**斜率优化或者凸优化** 这里显然是有凸性的,为什么呢,因为随着$$k$$越选越多,留给剩下的代价也会相应地增加 因为代价越小的优先被选走了 换句话说,$$f(k) = f(k-1) + cost_1, \ f(k-1) = f(k-2) + cost_2$$,那么$$cost_1 \geqslant cost_2$$ 实际上,这里我们没必要那么复杂,直接按照$$a(i) - a(i-1)$$排序,为什么呢? ```math \displaystyle a_r - a_l = (a_{l+1} - a_{l}) + (a_{l+2} - a_{l+1}) + \cdots + (a_{r} - a_{r-1}) ``` 实际上,一共有$$n-1$$个 gap,其中$$m-1$$个 gap 用不着统计,那么需要统计的只有$$n - m$$个 那我们找最小的$$n-m$$个差分值即可 ## leetcode 第 458 场周赛 ### C **[Q3. 用特殊操作处理字符串 II](https://leetcode.cn/contest/weekly-contest-458/problems/process-string-with-special-operations-ii/description/)** 给定一些操作,和一个整数`k`,如果是小写字母,那么复制到`res`中,如果是`*`,删除`res`最后一个字符 如果`#`,那么复制当前的`res`并追加到后面,`%`反转当前的`res` **算法分析** 类似平衡树,我们要追踪下标第`kth`的位置,那么预处理每一个下标处,`res`对应的实时`size` 然后考虑`dfs`,从`dfs(n)`开始(类似线段树之类的) 默认下标$$p \in [1, |S|]$$ 对于`dfs(p)`,如果`size(p) <= k`,那么无解,同时如果`p = 0`,也无解 如果$$S(p-1)$$恰好是一个字符,并且`size(p) - 1 = k`,那么`S[p-1]`就是答案 否则的话,继续在$$[1, p-1]$$区间里面找下标第`k`大 如果$$S(p-1)$$是`*`,继续在$$[1, p-1]$$找第`k`大 如果$$S(p-1)$$是`#`,说明**翻倍了,复制了一半**,每一半的大小是`half = size(p) / 2`,`k %= half` 然后继续在$$[1, p-1]$$找第`k`大 如果$$S(p-1)$$是`%`,对称地,找第$$k$$大变成了找第$$(size_p - 1 - k)$$大 ### D **[Q4. 图中的最长回文路径](https://leetcode.cn/contest/weekly-contest-458/problems/longest-palindromic-path-in-graph/description/)** **问题描述** 给定$$n$$个点的无向图,每个点有一个`label`,你可以从任意节点开始,每个点最多访问一次, 返回一条通过的路径,使得路径中的`label`构成回文串 **算法分析** 暴力,$$(mask, u, v)$$表示状态,其中$$mask$$表示一共选了哪些点?`u, v`分别表示路径的起点和终点 用`seen[mask][u][v]`表示状态是否访问过,没有访问过,就将其放入队列中,每次出队列的时候 用`ans = max(ans, popcount(mask))`来更新答案 初始的时候,每一个点单独成一个路径,`mask = (1<<u), seen[mask][u][u] = 1, ans = 1` 然后枚举`2`个点的情况,起点和终点,必须保证`x != y`,并且`label[x] == label[y]`,然后考虑状态`seen[mask][x][y]` 算法的核心是**枚举回文中心**,从回文中心向外扩展 每一次的回文中心,都是`que.front() = [mask, u, v]`,`[u...v]`构成了已有的回文中心 从`[u, v]`向外扩张,$$x \in g(u), y \in g(v)$$,如果`label[x] == label[y] 并且 x, y 都没有被加入的话` 那么`[x, [u, v], y]`就是新的回文串,加入队列中 ## Codeforces Round 856 (Div. 2) ### D **[D. Counting Factorizations](https://codeforces.com/contest/1794/problem/D)** **问题描述** 定义$$m$$的唯一分解是 ```math \displaystyle p_1^{e_1} p_2^{e_2} \cdots p_k^{e_k}, \quad p_1 < p_2 <\cdots < p_k ``` 其中$$p_1, p_2, \cdots, p_k$$都必须是素数 定义$$f(m)$$是多重集合,顺序不同可能会有不同的`m`,$$f(m) = \\{p_1, e_1, p_2, e_2, \cdots, p_k, e_k\\}$$ 现在问,给定$$2n$$个元素的序列$$a\_1, a\_2, \cdots, a\_{2n}$$,能够有多少种不同的$$m$$,满足$$f(m)$$恰好是$$a$$ **算法分析** 首先,序列中,非素数,只能作为幂指存在,剩下的,既可以是$$p$$,也可以是$$e$$ 可以先预处理,把素数和非素数分离开,分成两个集合,素数集$$|P|$$和指数集$$|pw|$$ 如果$$|P| < n$$,那么无解,因为不管怎么样都需要$$n$$个素数 否则的话,可以考虑`dp(i, k)`,表示考虑每个素数,$$i \in [1, m]$$,每个位置选或者不选,当前选了$$k$$个素数 ```math dp(i, k) \leftarrow dp(i-1, k) \\ dp(i, k) \leftarrow dp(i-1, k-1) \cdot (n - k + 1) ``` > 但这样并不正确,因为可供选择的指数种类,并不全是$$n$$,如果一些$$|P|$$中的元素没有被选上, 这些元素可能被加入到$$pw$$中,这会导致元素重复,比如`P = [2, 3, 5], pw = [2]`,不选`2`的话 实际上,`pw = {2, 2}`,看似是`2`种,实际上呢,只有一种选择 > 怎么做呢? 不难发现,实际上,$$pw = \\{2, 2, 3, 4, 5\\}$$中可能会有重复的元素,选择位置不同的`2`,算同一种方案 然后你要从中选$$n = 5$$个元素,作为**指数**,求方案数,这是个**多重集合全排列问题** ```math \displaystyle \dfrac{n!}{\prod_{i = 1}^{m} (cnt_i)!} ``` > 下面考虑用动态规划来做这个过程,用$$(x, cnt_x)$$表示`(具体的值x,x出现的次数)` 然后从小到大考虑每一个值 如果$$x$$**不是素数**,那么$$cnt_x$$必须全部贡献到答案中去,$$dp(i, k) \leftarrow dp(i-1, k) \cdot \dfrac{1}{(cnt_x)!}$$ 如果$$x$$**是素数**,不选$$x$$作为$$p$$的话,仍然$$cnt_x$$会全部贡献到答案中 此时$$dp(i, k) \leftarrow dp(i-1, k) \cdot \dfrac{1}{(cnt_x)!}$$ 选择$$x$$作为$$p$$,那么$$cnt_x$$只能贡献$$(cnt_x - 1)$$个 此时$$dp(i, k) \leftarrow dp(i-1, k-1) \cdot \dfrac{1}{(cnt_x - 1)!}$$ 最后$$dp(i, k) \cdot n!$$就是答案 ### E **[E. Labeling the Tree with Distances](https://codeforces.com/contest/1794/problem/E)** **问题描述** 给定一个$$n$$个节点的树,然后再给定$$n-1$$个数`a[1], a[2], ..., a[n-1]`,你可以用这些数给$$n$$个顶点标号 注意,一个数只能用一次,那么标号结束之后,会仅存在一个未标号的顶点,这个顶点你可以标上任意的数 我们定义一个顶点$$x$$是好的,当且仅当存在一种标号方式,使得**所有点**$$i$$的标号`lable[i]` 等于$$(i, x)$$之间的路径长度 现在需要输出所有好的顶点 **算法分析** 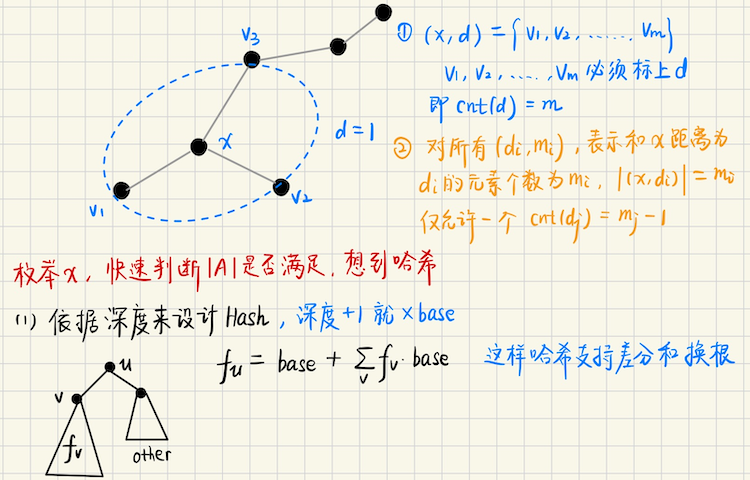 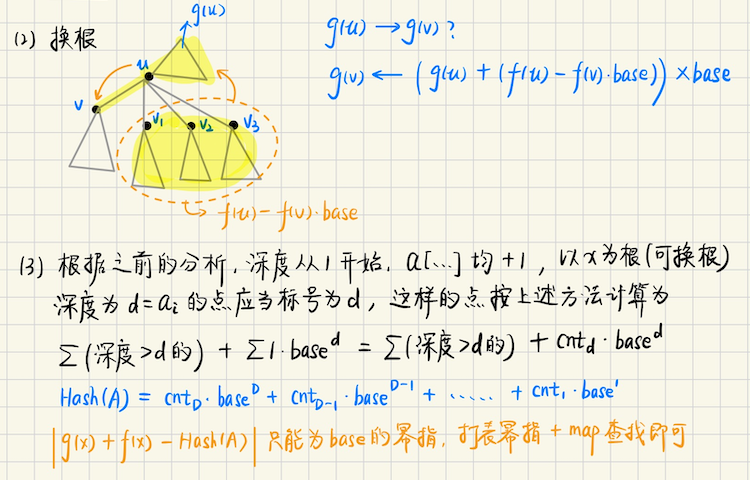 ## Codeforces Round 869 (Div. 2) ### C **[C. Almost Increasing Subsequence](https://codeforces.com/contest/1818/problem/C)** 如果不存在连续三个数$$x \geqslant y \geqslant z$$,那么这样的序列称为 almost incresing 的 现在给定`q`个询问,每个询问给定一个区间,问`[l, r]`最长的`almost incresing`的子序列长度是多少 子序列不要求连续 **算法分析** 不难发现,对于长度$$\geqslant 3$$的,连续递减的子序列,构成一段区间$$[l, r]$$,这样的区间最后只能保留`2`个数 于是我们可以预处理所有这样的区间,然后对于询问`[l, r]`,二分查找落在`[l, r]`区间中的`[li, ri]` 然后`tot = tot - sum`,把这些区间先减掉,然后再看一下减掉了`cnt`个这样的区间,`tot += 2 * cnt` > 但是会发现,这样写起来非常复杂,因为要考虑区间的端点,可能落一半在`[l, r]`端点处,怎么办? 实际上,一段发生$$\geqslant 3$$个元素连续递减的时候,这个位置才会被删除 我们可以维护连续递减的元素的个数,`dlen`,当`a[i-1] < a[i]`的时候,`dlen = 0` 否则`dlen += 1`,当`dlen >= 2`的时候,说明这个位置**需要被删除**,`del(i) = del(i-1) + (dlen >= 2)` 询问的时候,考虑`[l, r]`区间,`{l, l+1}`可以被保留,考虑`[l+2...r]`区间内,有多少个需要被删除的元素 > 总结,我们发现,对于完全落在区间$$[l, r]$$之间的若干个段$$[l_i, r_i]$$,要快速统计它们的和到底是多少? 这个时候二分有很多边界讨论,直接前缀和扫描,如果$$i$$处于段内,那么$$dp(i) = dp(i-1) + 1$$ 否则的话,$$dp(i) = dp(i-1)$$ 当然,按照我最开始的想法,也可以做,只不过麻烦一些,只有位于$$[l, r]$$区间内,若干个**完整的段**$$[l_i, r_i]$$ 需要按照`tot = tot - calc(完整段总长度) + 2 * cnt`,其中`cnt`表示有几个完整的段 首尾的段可能不完整,需要单独处理,当且仅当`len > 2`的时候,`tot -= len, tot += 2`,否则不处理 ## 2025牛客暑期多校训练营2 ### A **[Another Day of Sun](https://ac.nowcoder.com/acm/contest/108299)** **问题描述** 给定一个序列,都是`{0, 1, -1}`,现在呢,对于所有的`-1`,你可以改成`0 or 1` 这样会构造若干个不同的序列,每一个序列有多少个相邻的`(0, 1)`段?对每个序列求这样一个值 然后对这些值求和,是多少? **算法分析** 考虑$$dp(i, 0/1)$$表示在`i`位置,以`0 or 1`结尾的,有$$dp(i, 0/1)$$个相邻的`(0, 1)`段 对于$$a_i = 0, 1$$的情况,转移是确定的 如果$$a_i = 0$$,那么不管怎么样,都不会使得已有的段变长,`dp(i, 0) = dp(i-1, 0) + dp(i-1, 1)` 注意到,如果$$a_i = -1$$,那么改成`{0, 1}`,相当于在原来的基础上,创建了一个不同的分支 之后呢?你`+1`,对答案的贡献就不是`+1`了,而是`+ 1 * (分支方案数)` 如果前面有$$k$$个$$-1$$,实际上,会形成$$2^k$$不同的分支,那么$$ways = 2^k$$,如果序列长度增长 对答案的贡献是`+ways` 所以如果$$a_i = 1$$,那么`dp(i, 1) = ( dp(i, 0) + ways ) + dp(i, 1)` ### L **[Love Wins All](https://ac.nowcoder.com/acm/contest/108299/L)** **问题描述** 偶数个点,给定若干个环,然后你可以删除两个点,要求剩下的点两两匹配,并且两个点之间有连边的才能算是一个匹配 问得到不同匹配的方案数 **算法分析** > 每位居民$$i$$在社区中都有一个他/她非常爱的居民$$a_i$$,并且每两个居民爱着不同的居民 等价于每个点的入度都是`1`,那么$$(i, a_i)$$连边,原图一定构成若干个环 并且偶数个点,所以奇环的个数必须是偶数 最后想要两两配对,那么是一个二分图,奇环是不能被保留的 > 若有$$\geqslant 4$$个奇环,那么你删除`2`个点,最多最多就删掉`2`个奇数环,剩下的奇环$$\geqslant 2$$,无解 那么单独考虑奇环个数为`2`的情况,删去的`2`个点,一定是这两个奇环各删一个点 所以删点的方案数是$$res = |C_1| \cdot |C_2|$$ 那么奇环破环成链了,剩下的选择方案是唯一的,仅剩下一条链,方案数就是`1`,$$(i, i+1)$$匹配就可以了 那么偶环呢?偶环可以顺时针绕,也可以逆时针绕,一共是`2`种方案,所以答案是$$res \cdot 2^{k}$$ 特别地,如果是二元环,方案数是`1`,所以$$k$$是**非二元偶环的个数** > 如果没有奇环呢? 那么我们删点,就一定是在同一个偶环上,选`2`个点删,怎么删? 可以对偶环进行黑白二染色,为了使得二分图仍然有最大匹配,一定是黑点选一个删,白点选一个删 删点的方案数是$$\dfrac{|C|}{2} \cdot \dfrac{|C|}{2}$$,其中$$|C|$$是环的大小 删了之后,偶环成了`2`条长度为偶数的链,匹配方案是唯一的 (Hall 定理,完全浸润) 所以删除的这个环,对答案的贡献是 $$\dfrac{|C|}{2} \cdot \dfrac{|C|}{2}$$ 我们就枚举删除哪个环即可,然后加起来 还有呢?考虑剩余的环做匹配,可能还会剩余若干个偶数环,剩余的贡献是$$2^{k - 1}$$ 两个乘起来即可 ## 2025 杭电多校 ### 1009 **[苹果树](https://acm.hdu.edu.cn/contest/problem?cid=1173&pid=1009)** 给定$$n$$个节点的树,每个点有一个点权,有$$m$$次操作,每次操作形如 `1 x y`,查询`x, y`路径上的最大点权 `2 x z`,对所有和`x`相连的点$$i$$,令$$a_i \leftarrow a_i + z$$ **算法分析** 不难想到树链剖分,查询`1`很好解决,查询`2`呢? 注意到,由于点的度数很大,不太能直接暴力修改,怎么办呢? 实际上,`HLD`最后搞出来若干段**重链**,不难发现,重链上基本都是重儿子 是不是只要暴力修改两个点,$$x$$的重儿子,$$x$$的父亲,就可以了呢? 这几乎是对的,唯一的缺憾是,对于每条**重链的链头元素**,它是轻儿子,那么轻儿子怎么办? 一个点$$x$$可能有非常多的轻儿子 我们的想法是,不暴力改轻儿子,而是直接把轻儿子发生的修改,在它**父亲处**结算 也就是说,我们在`x`上,维护一个`add(x)`,表示轻儿子总共要被加的量是多少? 然后可以标记**链的端点,是不是重儿子**,如果链的端点是**轻儿子**,那么`fa = hld.pa[u]` 线段树上查询轻儿子的`a`的值是多少,假设说是`res`,`res + add[fa]`和`ans`再取一个`max`即可 ## 2025牛客暑期多校训练营3 ### H **[Head out to the Target](https://ac.nowcoder.com/acm/contest/108300/H)** **问题描述** 给定$$n$$个节点的树,一开始你在`根节点 1`,给定若干询问$$[l_i, r_i, u_i]$$ 表示在$$[l_i, r_i]$$,节点$$u_i$$出现一个目标,如果任何时刻有目标出现,并且你和目标在一个连通块内 你如果不和目标重合的话,可以朝目标的方向移动一步,如果重合了,就不会动了,游戏结束 你可以在任何时刻,包括时刻`0`,切掉树中任意数量的边,可以执行多次 现在问,你能重合于某个目标的最早时刻 **算法分析**  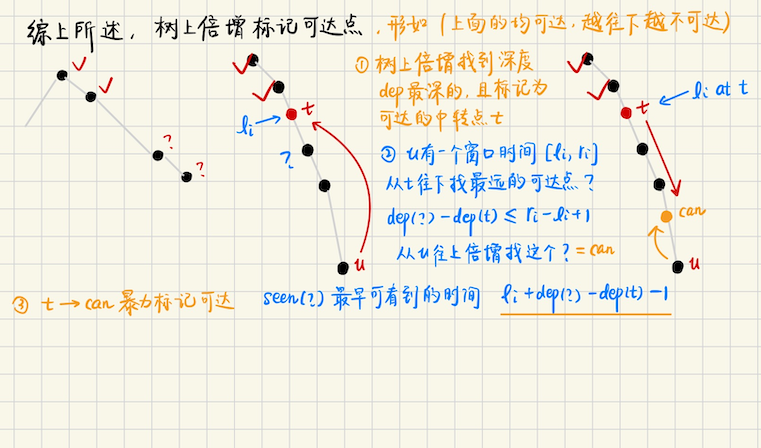
0
0
上一篇:七月算法竞赛选题(一)
下一篇:七月算法竞赛选题(三)
看完文章有啥想法
发布评论
520 人参与,0 条评论