五月算法竞赛选题（二）

[[ slider_text ]]

[[ item.c ]]

五月算法竞赛选题（二）

发布时间 2025-06-04 作者：秋千月 来源：算法小站

排列与置换 数形结合

## Codeforces Round 1025 (Div. 2)
### D
**[D. D/D/D](https://codeforces.com/contest/2109/problem/D)**
给你一个无向图，和一个集合 A，只要 A 非空，你就可以做以下操作任意次
选择一个 A 中的一个元素比如是$$a_k$$，然后在 A 中删掉$$a_k$$，并且在无向图上行走恰好$$a_k$$条边
现在问你能不能从起点`1`，经过若干次操作，到达点$$u$$，注意，可能会重复经过某些中间点
每个点之间的询问是独立的

**算法分析**
不难发现，如果**最短路**$$dist(1\to u) > \sum A$$的话，不论如何也不可能
否则的话，比如你到达$$i$$点，你可以在$$i \to j \to i$$上，消耗掉多余的边，$$d \to d + 2k$$
不难发现**奇偶性**是不变的

那么考虑拆点，每个点$$(u, 0), (u, 1)$$表示经过偶数/奇数 step 可达
如果$$sum = \sum A$$是**奇数**并且$$\geqslant dist(u, 1)$$，那么一定可以，偶数同理

否则，我们要尝试让$$sum$$改变一下奇偶性，同时要让$$sum$$**尽可能大**
我们就找到**最小的奇数**`mnodd`，$$sum \leftarrow sum - mnodd$$，然后再判断一下

### E
**[E. Binary String Wowee](https://codeforces.com/contest/2109/problem/E)**
给你一个`01`串，你每次可以选择一个$$i$$，需要满足$$s_i = 0$$，然后翻转前缀$$s[1\cdots i]$$
你需要执行这样的操作恰好`k`次，问最后能得到多少个**不同的操作序列**，答案对`998244353`取模

注意是不同的操作序列，不是不同的串，对于第$$i$$次操作，如果两个操作序列第$$i$$次，
作用于不同的下标`idx`，我们就认为这两个操作序列是不同的

**算法分析**
> 状态设计比较套路，$$dp(i, k)$$表示在$$i$$位置，当前发生了$$k$$次操作的方案数
难点是怎么去递推

一种想法是，考虑这个修改的过程，假设修改了$$i$$，然后呢？我们要在$$j \in [1\cdots i-1]$$这样的前缀中
再次修改，这样看上去好像很难做

我们可以一个一个点考虑，比如当前一共发生了$$m$$次操作，在$$i$$处恰好发生了其中的$$k$$次
这样$$\displaystyle \binom{m}{k}$$去递推好像可以？
这个过程，修改$$i$$，然后再修改它的前缀$$i-1 \to 1$$，不难发现应该**倒着递推**

> 状态转移

枚举$$i+1$$的修改次数$$dp(i+1, k1)$$

1.如果$$i$$位置不发生任何修改，$$dp(i+1, k1) \to dp(i, k1)$$
2.否则的话，枚举$$i$$发生的修改次数$$k2 \in [k1+1, m]$$（`m`是总共允许的修改次数）

存在转移$$\displaystyle dp(i+1, k1) \cdot \binom{k2}{k2 - k1}$$，即恰好有任意的$$|k2-k1|$$次是发生在$$i$$身上的

这样几乎就做完了，但是还有一个问题，就是它存在限制，$$i$$位置能发生修改，当且仅当$$s_i = 0$$
那么得考虑奇偶性

1.如果$$s_i = 0$$，那么$$(k2 - k1)$$次修改中，$$0 \to 1 \to 0 \to \cdots$$，只有$$\lceil\dfrac{tot}{2} \rceil$$次才是被允许的
`tot`表示总共需要的**翻转次数**

换句话说，如果在$$i$$处恰好发生了$$l$$次修改，总共可能要操作$$2l$$次这么多，具体来说
考虑前缀$$[1\cdots i]$$，总共发生的翻转次数是$$k1 + l$$次，其中只有$$\lceil (k1 + l) / 2 \rceil$$
这么多次，能够用于操作$$i$$这个位置

所以只能$$\displaystyle \binom{ \lceil (k1 + l)/2 \rceil}{l}$$，其中$$l \in [1\cdots ]$$，满足$$k1+l \leqslant m$$

2.如果$$s_i = 0$$，那么对应$$\displaystyle \binom{\lfloor (k1 + l) / 2 \rfloor}{l}$$

```math
\displaystyle
\binom{ \lceil (k1 + l)/2 \rceil}{l} \cdot dp(i+1, k1) \to dp(i, k1 + l)
```

## Codeforces Round 1026 (Div. 2)
### C
**[C. Racing](https://codeforces.com/contest/2110/problem/C)**
**问题描述**
无人机，一开始在高度`0`处，现在给你一个数组$$d$$，`d[i]`表示，`h[i] = h[i-1] + d[i]`
无人机可以上升$$d_i$$高度，现在对每个`i`，给定一个$$[l_i, r_i]$$，表示无人机高度的限制
但是$$d$$数组缺少了一部分值不知道，$$d$$数组每个值都是`0 or 1`，无人机只会升高，不会下降
现在问，能不能构造一个`d`，补上缺少的部分，使得无人机能够顺利通过每个点？

**算法分析**
这个题可以用数形结合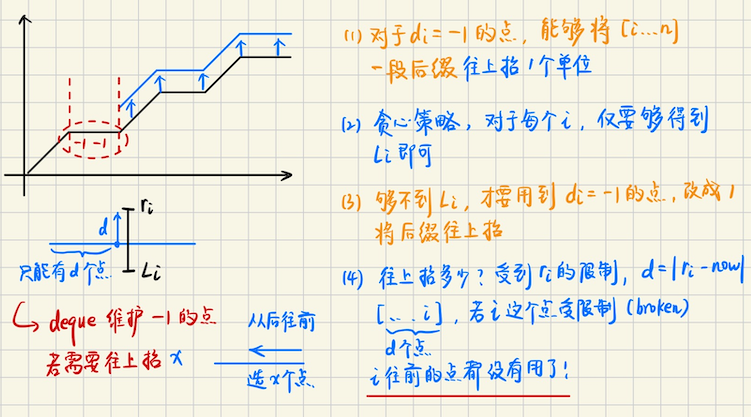
![](/media/content_img/cf1026c.png)

## Codeforces Round 1024 (Div. 2)
### D
**[D. Quartet Swapping](https://codeforces.com/contest/2102/problem/D)**
**算法描述**
给你一个`n`的排列`a`，你可以执行以下操作任意多次
选择一个$$1 \leqslant i \leqslant n - 3$$，**同时交换**$$(a\_{i}, a\_{i+2})$$和$$(a\_{i+1}, a\_{i+3})$$
现在你要通过上述操作，使得字典序最小，输出这个最小的字典序

**算法分析**
1.实际情况是，奇数位和奇数位交换，偶数位和偶数位交换
**理想情况**，奇数位排个序，偶数位排个序，但是因为这里要求**同时交换**，理想情况不一定可以取的到

2.注意到给定的是一个排列，也就是说，对于每个值，**它要去的位置是固定的**（在排序后的序列中）
总共要走的距离，是序列**逆序对的个数**，那么考虑什么时候不能满足呢？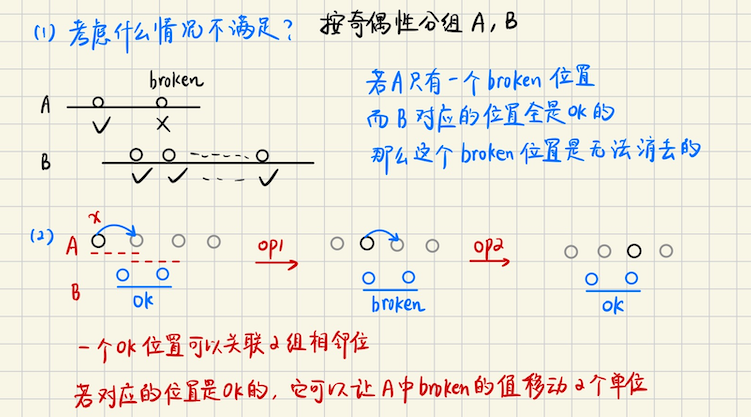
![](/media/content_img/cf1024d1.png)
![](/media/content_img/cf1024d2.png)

## Codeforces Round 1028
### D
**[D. Gellyfish and Camellia Japonica](https://codeforces.com/contest/2116/problem/D)**
**问题描述**
你有一个序列，一开始是$$c = [a_1, a_2, \cdots, a_n]$$，然后$$q$$次修改
第$$i$$次修改，给定$$(x_i, y_i, z_i)$$，令$$c(z_i) = \min(c(x_i), c(y_i))$$
修改之后，$$c$$序列最终变成了$$[b_1, b_2, \cdots, b_n]$$，现在$$q$$次修改和$$b$$已知
要你构造一个可能的$$a$$，或者输出不存在合法的$$a$$

**算法分析**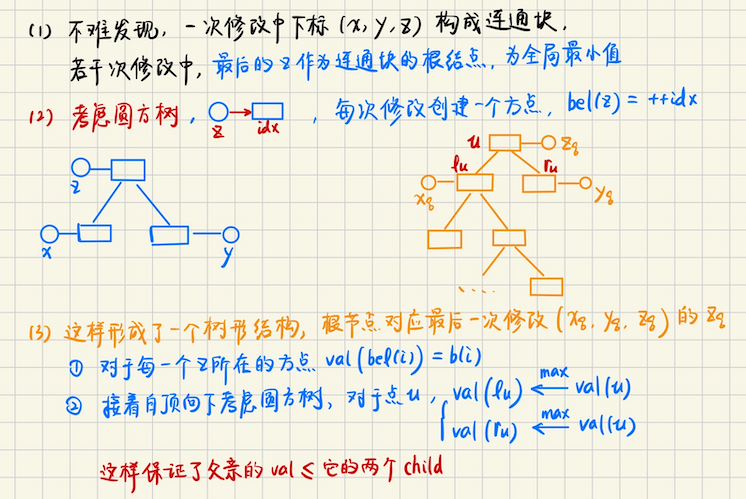
![](/media/content_img/cf1028d.png)

## 数形结合
### Three Arrays
**[Three Arrays](https://codeforces.com/contest/1940)**
**问题描述**
给定长度为$$n$$的序列$$D, L, R$$，下标从`1`开始，同时给定$$a_0, b_0$$
现在你需要按照如下方式构造长度为$$n+1$$的序列$$A, B$$

1.$$A_0 = a_0, B_0 = b_0$$

2.对于每一个$$i \in [1, n]$$，执行以下操作，首先$$A\_{i} = A\_{i-1}+D\_{i}, B\_{i} = B\_{i-1} + D\_{i}$$

然后选择其中一种操作，$$A_i = \min(A_i, L_i)$$或者是$$B_i = \min(B_i, R_i)$$
现在要使得$$A_n + B_n$$尽可能大，输出这个最大值

**算法分析**
> 注意到$$a_0, b_0, D$$是确定的，并且操作只会减小他们的值，所以理想情况就是不需要操作

如果$$A_i \leqslant L_i$$或者$$B_i \leqslant R_i$$，在$$i$$这个位置是不需要操作的
否则就一定会操作

> 那么操作会影响什么呢？考虑数形结合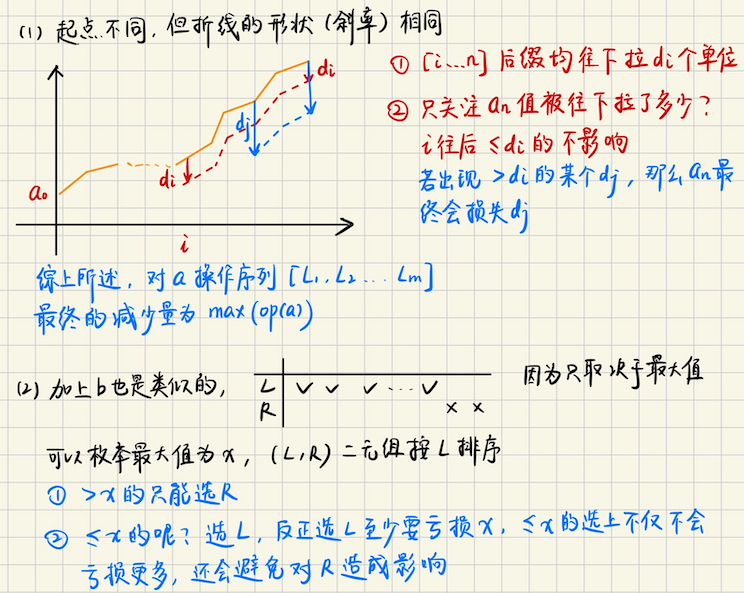

![](/media/content_img/threearrays.png)

**算法实现**
可以先对二元组排序，然后用一个`multiset`来维护`R`中的所有后缀
从前往后`for i in L`，每考虑一个`i`，就需要在`multiset`中把`R[i]`动态删除，然后求最大值
```bash
void solve(int cas) {
    int n;
    cin >> n;

vector<i64> D(n+1, 0), L(n+1, 0), R(n+1, 0);
    for (int i = 1; i <= n; i++) cin >> D[i];
    for (int i = 1; i <= n; i++) cin >> L[i];
    for (int i = 1; i <= n; i++) cin >> R[i];

vector<i64> a(n+1, 0), b(n+1, 0);
    cin >> a[0] >> b[0];

using pii = pair<i64, i64>;

for (int i = 1; i <= n; i++) {
        a[i] = a[i-1] + D[i];
        b[i] = b[i-1] + D[i];
    }

vector<pii> op;
    for (int i = 1; i <= n; i++) {
        if (L[i] >= a[i] || R[i] >= b[i]) continue;

i64 dx = a[i] - L[i];
        i64 dy = b[i] - R[i];

op.push_back(pii{dx, dy});
    }

sort(op.begin(), op.end());

multiset<i64> st;
    for (auto [x, y] : op) st.insert(y);

i64 expect = a[n] + b[n];
    i64 res = expect - (st.size() == 0 ? 0 : *st.rbegin());

for (int i = 0; i < op.size(); i++) {
        auto [x, y] = op[i];

i64 now = expect - x;
        st.erase(st.find(y));
        now -= (st.empty() ? 0 : *st.rbegin());
        chmax(res, now);
    }

cout << res << "\n";
}
```

上一篇：同余与模的一些问题下一篇：六月算法竞赛选题——概率与期望（一）

看完文章有啥想法