四月算法竞赛选题（二）

[[ slider_text ]]

[[ item.c ]]

四月算法竞赛选题（二）

发布时间 2025-05-02 作者：zhangminchen 来源：算法小站

二维数点

## Codeforces Round 1004 (Div. 2)
### E
**[E. White Magic](https://codeforces.com/contest/2067/problem/E)**
**问题描述**
定义一个序列`a[1...n]`是`magic`的，当且仅当对于**所有的**$$1 \leqslant i \leqslant n-1$$，均有$$\min(a\_1, \cdots, a\_i) \geqslant mex(a\_{i+1}, \cdots, a\_n)$$

特别地，任何长度为`1`的序列都是`magic`的

给定$$n$$个非负整数的序列`a`，求解可能的，**最长的 magic 子序列**的长度，子序列不需要连续

**算法分析**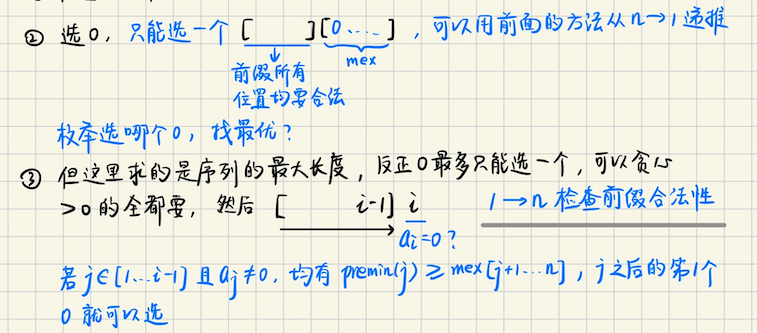
![](/media/content_img/cf1004e1.png)
![](/media/content_img/cf1004e2.png)
![](/media/content_img/cf1004e3.png)

> 注意这题 **dp 不可以做**

为什么呢？对每个位置$$i$$，可以$$dp(i, 0/1)$$表示选或者不选，**但是，**我们不知道`[i+1...n]`中
每个位置选或者不选，对应的`mex`值是多少，这个是不知道的，不能 dp

## Codeforces Round 1019 (Div. 2)
### C
**[C. Median Splits](https://codeforces.com/contest/2103/problem/C)**
给定一个数组，把数组划分成`[1...l], [l+1...r], [r+1...n]`三个部分，问是否存在这样的划分，满足
```math
med(med(a_1 \cdots a_l), med(a_{l+1}\cdots a_{r}), med(a_{r+1}\cdots a_n)) \leqslant k
```
其中`med`表示中位数，即排序后，下标$$\lceil \dfrac{len}{2} \rceil$$位置的元素

**算法分析**
> 存在的充要条件是什么？

此类问题，一般如果是`exists`问题，$$\leqslant k$$，可以转化成，**区间**$$\min \leqslant k$$
那么不难发现，满足$$med \leqslant k$$的，`[pre, mid, suf]`，**满足条件的区间段数**，一定会$$\geqslant 2$$

这样的问题，可以将其转化，$$\leqslant k, \text{then } b_i = +1$$，$$> k, \text{then } b_i = -1$$
对`b`数组求前缀和，后缀和`pre[...], suf[...]`

> 枚举前缀

前缀合法，当且仅当$$pre_i \geqslant 0$$

枚举前缀$$i$$，考虑是否$$\exists j \in [i+1, n]$$，满足$$[i+1, j]$$合法，即$$pre_j - pre_i \geqslant 0$$
那么只需要$$(\max pre_j \mid j \in [i+1, n]) \geqslant pre_i$$即可，区间最大值`ST`表就可以搞定
上述值记为`maxmid`

然后考虑后缀$$suf_j$$， 如果$$(\max suf_j \geqslant 0 \mid j \in [i+2, n])$$，那么也是可以满足的
上述值记为`maxsuf`

如果$$pre_i \geqslant 0$$，那么只需要`maxmid >= 0 or maxsuf >= 0`
如果$$pre_i < 0$$呢？此时后缀一定必须$$\geqslant 0$$，**对称地，枚举后缀即可**

> 对称地，对后缀再做一遍枚举即可

## Codeforces Round 1004 (Div. 2)
### D
**[D. Object Identification](https://codeforces.com/contest/2067/problem/D)**
**问题描述**
给你一个序列`x[1...n]`，同时有一个确定的序列`y[1...n]`，所有的数范围都是`[1...n]`
但是呢，`y`中的数具体是多少你不知道，你只知道对于所有的$$i$$，均有$$x_i \neq y_i$$
并且呢，所有的$$(x_i, y_i)$$二元组都是不同的

现在呢，jury 有 2 种想法
第一种，它根据`x, y`建了个有向图，$$n$$条边，每条边都是$$x_i \to y_i$$
第二种，在平面中建立坐标$$(x_i, y_i)$$

现在要交互，你可以询问，每次询问给出$$(i, j)$$，如果是第一种想法，那么会返回点$$i \to j$$的最短路径
如果没有路径，那么返回`0`

如果是第二种想法，那么返回$$(x_i, y_i), (x_j, y_j)$$的曼哈顿距离
但是你只能问 2 个问题，确定是哪种想法

**算法分析**
> 这个问题不难，冷静分析一下，自己也独立想出来了

首先考虑，如果`a`**不是排列**，那么可以找到$$[1\cdots n]$$中，没有在`a`中出现的数，假设说是`id1`
然后另外找到一个出现在`a`中的数`id2`，询问`(id1, id2), (id2, id1)`

如果是`Dijkstra`，那么答案一定是`0`，否则就是`Manhatom`距离

于是只需要考虑排列的情况
那如果是排列，不放先假设说是曼哈顿距离，我们找到`1 and n`所在的位置，`p = pos[1], q = pos[n]`
然后询问`(p, q), (q, p)`

分为一下几种情况
如果是曼哈顿距离，答案一定$$\geqslant n - 1$$，如果`< n-1`，那么一定是`Dijkstra`了
如果`> n - 1`呢？肯定是`Manhatom`了，因为$$n$$个点的排列，最短路肯定不会超过`n-1`的

接下来只要考虑答案是$$n - 1$$的情况了，如果是`dijkstra`说明什么呢？
那么此时一定$$p, q$$连到同一个点上，构成一个**环 + 外向树**的结构，此时$$dist(p, q) \neq dist(q, p)$$
如果问题返回二者相等，那么一定是`Manhatom`距离，否则就是`Dijkstra`

## Codeforces Round 1021 (Div. 2)
### C. Sports Betting
**[C. Sports Betting](https://codeforces.com/contest/2098/problem/C)**
**问题描述**
给你很多个连续的整数点，每个点的值都可能是`0 or 1`，但是你一开始不知道这些点是多少，它随机是`0 or 1`
现在你有`n`个学生，每个学生$$x = a_i$$，表示你对第$$i$$个学生，进行点$$x+1,x+2$$值的猜测
你被认为成功，当且仅当**至少一个学生**，他需要知道的两个点$$x+1, x+2$$，答案是正确的

现在你要安排一种策略，比如`a[1] = 5`，那么你给第一个学生答案，告诉他你觉得第`6, 7`个数可能的值，比如说是`(0, 1)`或者`(1, 0)`等等
那么问，存不存在一种策略，使得**至少一个学生**，一定能给出正确答案？

**算法分析**
> 首先，如果发现$$cnt \geqslant 4$$的数，那么一定会成功

考虑其他情况
![](/media/content_img/cf1021c.png)

## Codeforces Round 986 (Div. 2)
### D
**[D. Alice's Adventures in Cards](https://codeforces.com/contest/2028/problem/D)**
**问题描述**
Alice 和 Queen, King, Jack 玩纸牌游戏（以下简称 Q, K, J），纸牌游戏一共有`n`种牌，Alice 现在有一张牌 1，
他希望通过交易得到牌`n`，其他玩家每种牌各有一张

现在有如下交易规则，每个人用一个`1-n`的排列，来表示对于每种牌的偏好程度，比如$$p_3 = 5$$，表示对第`3`张牌的偏好值是`5`
如果$$p_a > p_b$$，那么这个人更愿意用自己手中的`b`，去和 Alice 手中的`a`进行交换
但是 Alice 就不一样了，Alice 总是偏好类型大的牌，换句话说，如果$$a > b$$，Alice 总是偏好牌$$a$$

现在问 Alice 得到牌`n`是否可能，如果可能，给出操作序列

![](/media/content_img/cf986d.png)

> 本题比较有意思的是，用**树状数组 + 二位数点**，来模拟建图的过程，如果存在$$x \to y$$的边
那么才需要在对应的树状数组上，执行`add(p[y], 1)`

输出方案，因为是排列，并且整个换牌的过程，是从小到大换的，一个牌只会被换一次，所以从小到大暴力检查一遍即可
只要当前状态合法，那么一定能被换到

从大到小检查，一个数只会被检查一次，记上一个数是`last`，如果`for y = n to 1`，有`p[y] > p[last]`
那么`y`就可以被换到，看一下`Q, K, J`哪一个满足即可

**算法实现**
```bash
using pii = pair<int, char>;

void solve(int cas) {
    int n;
    cin >> n;

vector<int> Q(n+1, 0), K(n+1, 0), J(n+1, 0);
    for (int i = 1; i <= n; i++) cin >> Q[i];
    for (int i = 1; i <= n; i++) cin >> K[i];
    for (int i = 1; i <= n; i++) cin >> J[i];

Fenwick<int> tq(n+5), tk(n+5), tj(n+5);

vector<int> dp(n+5, 0);
    dp[1] = 1;

for (int y = 1; y <= n; y++) {
        int cq = n + 1 - Q[y];
        int ck = n + 1 - K[y];
        int cj = n + 1 - J[y];

auto sq = tq.sum(cq);
        auto sk = tk.sum(ck);
        auto sj = tj.sum(cj);

dp[y] |= (sq | sk | sj);

if (dp[y]) {
            tq.add(cq, 1), tk.add(ck, 1), tj.add(cj, 1);
        }
    }

if (dp[n] == 0) {
        cout << "NO\n";
        return;
    }

int now = n;
    vector<pii> ans;
    // ans.push_back(now);

for (int y = n-1; y >= 1; y--) {
        if (dp[y] == 0) continue;

if (Q[y] > Q[now]) {
            ans.push_back(pii{now, 'q'}), now = y;
            continue;
        }

if (K[y] > K[now]) {
            ans.push_back(pii{now, 'k'}), now = y;
            continue;
        }

if (J[y] > J[now]) {
            ans.push_back(pii{now, 'j'}), now = y;
            continue;
        }
    }
    reverse(ans.begin(), ans.end());
    cout << "YES\n";
    cout << ans.size() << "\n";
    for (auto [v, tp] : ans) {
        cout << tp << " " << v << "\n";
    }
}
```

上一篇：四月算法竞赛选题（一）下一篇：同余与模的一些问题

看完文章有啥想法